Sign In

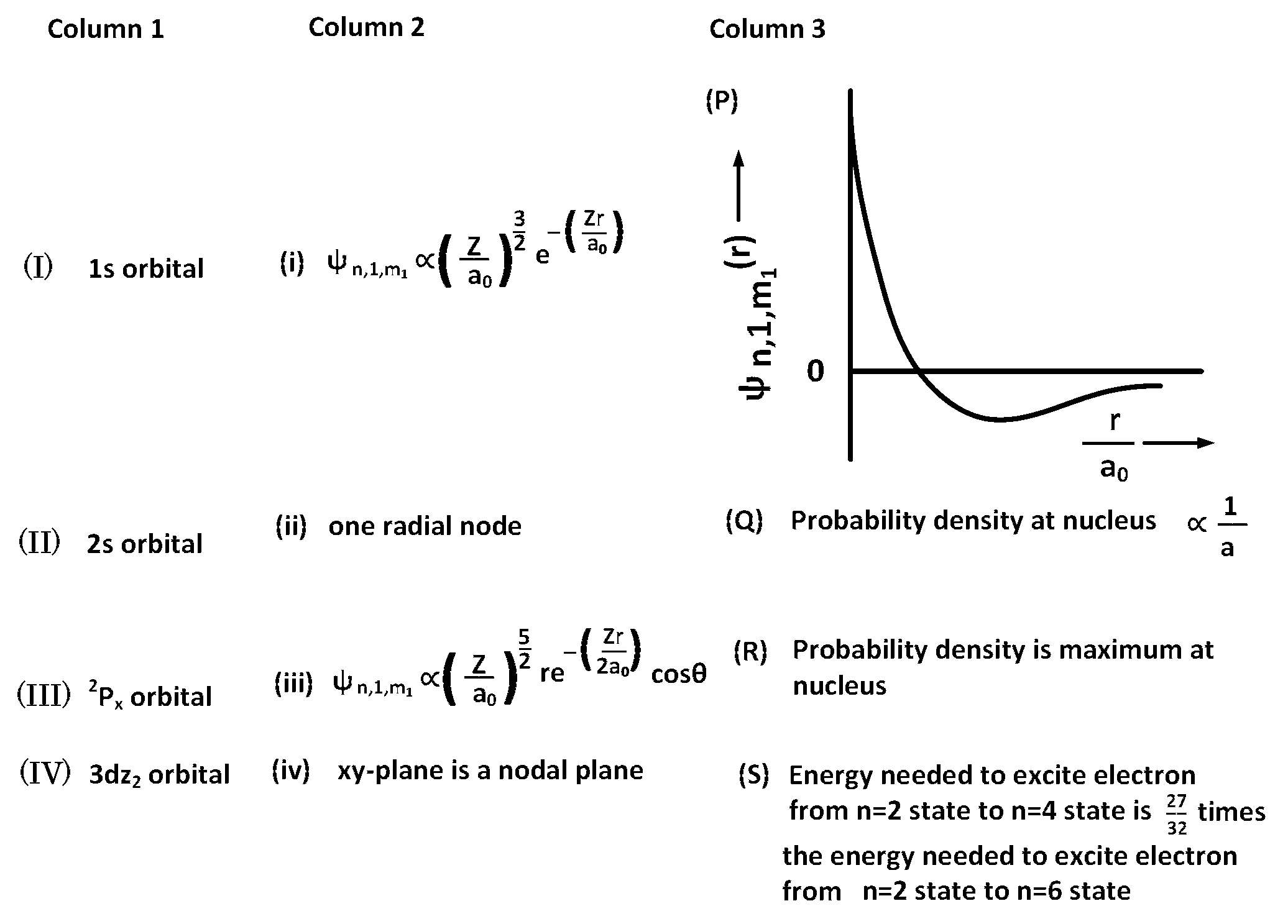
JEE Advance - Chemistry (2017 - Paper 1 Offline - No. 18)

The wave function, $${\psi _{n,1,{m_1}}}$$ is a mathematical function whose value depends upon spherical polar coordinates $$\left( {r,\theta ,\phi } \right)$$ of the electron and characterized by the quantum numbers $$n,1$$ and $${m_1}$$. Here $$r$$ is distance from nucleus, $$\theta $$ is colatitude and $$\phi $$ is azimuth. In the mathematical functions given in the table, $$Z$$ is atomic number and $${a_0}$$ is Bohr radius.

The wave function, $${\psi _{n,1,{m_1}}}$$ is a mathematical function whose value depends upon spherical polar coordinates $$\left( {r,\theta ,\phi } \right)$$ of the electron and characterized by the quantum numbers $$n,1$$ and $${m_1}$$. Here $$r$$ is distance from nucleus, $$\theta $$ is colatitude and $$\phi $$ is azimuth. In the mathematical functions given in the table, $$Z$$ is atomic number and $${a_0}$$ is Bohr radius.

The wave function, $${\psi _{n,1,{m_1}}}$$ is a mathematical function whose value depends upon spherical polar coordinates $$\left( {r,\theta ,\phi } \right)$$ of the electron and characterized by the quantum numbers $$n,1$$ and $${m_1}$$. Here $$r$$ is distance from nucleus, $$\theta $$ is colatitude and $$\phi $$ is azimuth. In the mathematical functions given in the table, $$Z$$ is atomic number and $${a_0}$$ is Bohr radius.

For the given orbital in Column 1, the only CORRECT combination for any hydrogen-like species is :
(I) (ii) (S)
(IV) (iv) (R)
(II) (ii) (P)
(III) (iii) (P)

Explanation

- Option (A) : Incorrect. The total number of radial nodes is given by $n-l-1$. For $1 s$ orbital, the radial node is zero (i.e. $1-0-1=0$ ).

- Option (B) : Incorrect. $d_{z^2}$ orbital has two lobes that point in opposite directions along $z$-axis plus a doughnut-shaped ring of electron density around the centre that lies in the $x y$-plane. Therefore, it does not have any nodal plane.

- Option (C) : Correct. The total number of radial nodes is given by $n-l-1$.

For $2 s$ : Radial nodes $=2-0-1=1$

The orbital 2s of hydrogen like species can be diagrammatically represented as :

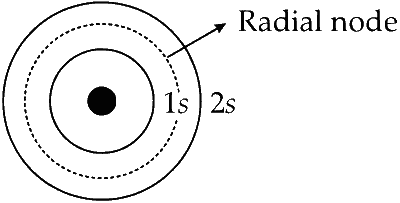
JEE Advanced 2017 Paper 1 Offline Chemistry - Structure of Atom Question 12 English Explanation 1
There is a spherical region of zero electron density between $1 s$ and the $2 s$ orbital of hydrogen like species. This spherical region is called the node. Only one radial node exist between $1 s$ and $2 s$.

The plot of wave function for $2 s$ verses radial distance from the nucleus is represented as

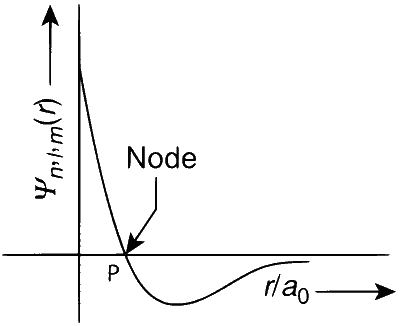
JEE Advanced 2017 Paper 1 Offline Chemistry - Structure of Atom Question 12 English Explanation 2

Point $P$ represents the region of zero electron density at a distance $r$ from the nucleus. This represents spherical node.

- Option (D) : Incorrect. The probability density at nucleus is for $2p$ orbital is zero.

Comments (0)

Advertisement