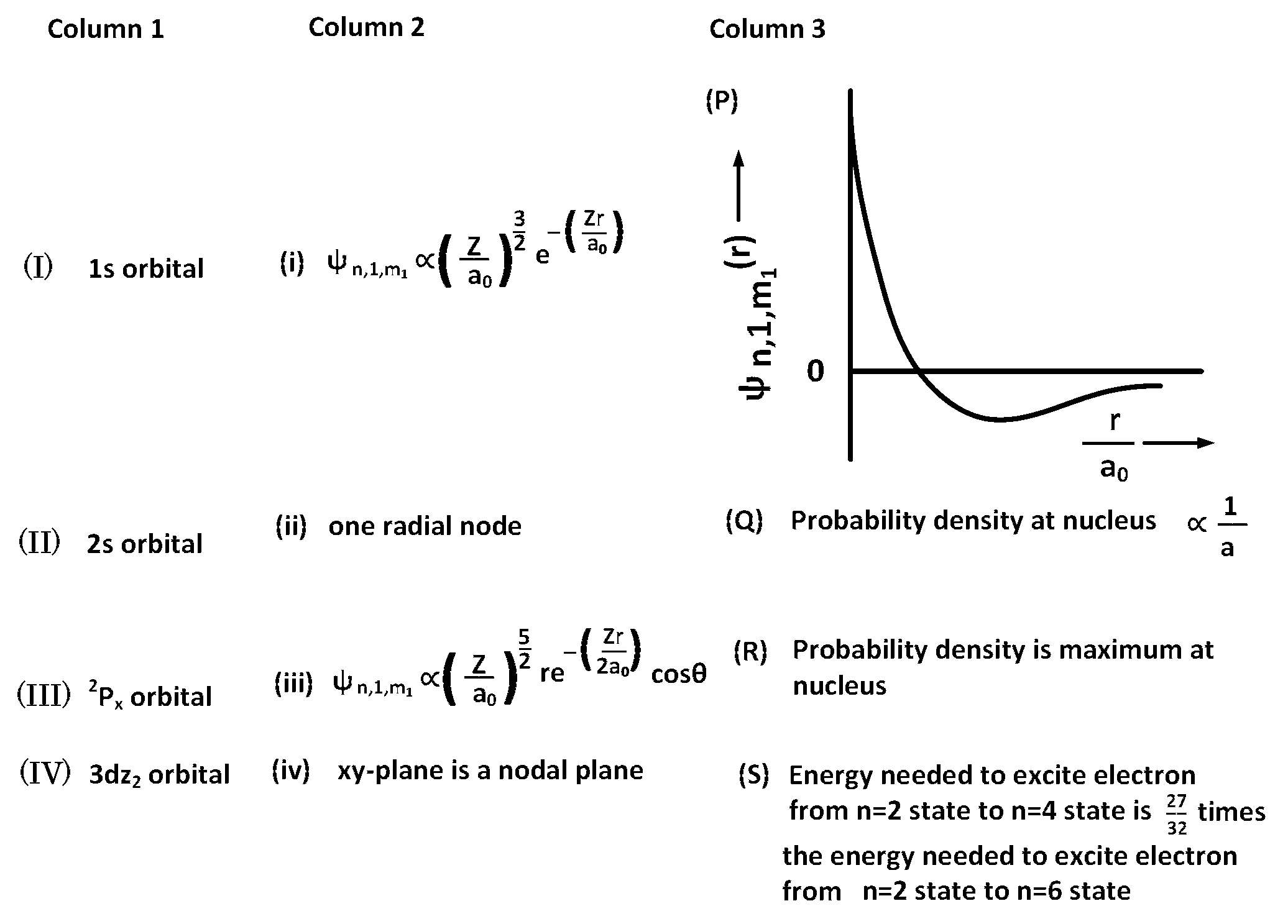
JEE Advance - Chemistry (2017 - Paper 1 Offline - No. 17)
For hydrogen atom, the only CORRECT combination is :
(I) (i) (S)
(II) (i) (Q)
(I) (i) (P)
(I) (iv) (R)
Explanation
(i) Wave function for 1s orbital of hydrogen atom with $n, l$ and $m_l$ as quantum numbers is given
$$ \psi_{n, l, m_l}=\frac{1}{\sqrt{\pi}}\left(\frac{Z}{a_0}\right)^{3 / 2} e^{-Z r / a_0} $$
Where, $\mathrm{Z}$ is atomic number of the element, $r$ is the variable distance of electron from the nucleus, $a_0$ is the Bohr's radius
For $1 \mathrm{~s}$ orbital, $n=1, l=0, m_l=0$ and wave function is represented as :
$$ \begin{aligned} & \psi_{1,0,0}=\frac{1}{\sqrt{\pi}}\left(\frac{Z}{a_0}\right)^{3 / 2} e^{-Z r / a_0} \\\\ \Rightarrow \psi_{1,0,0} & \propto\left(\frac{Z}{a_0}\right)^{3 / 2} e^{-Z r / a_0} \end{aligned} $$
(ii) Energy of excitation of electron from $n_1=2$ to $n_2=4$ is given as :
$$ \begin{aligned} & \mathrm{E}_{2 \rightarrow 4} \propto-\mathrm{R}\left(\frac{1}{n_2^2}-\frac{1}{n_1^2}\right) \\\\ & \mathrm{E}_{2 \rightarrow 4} \propto-\mathrm{R}\left(\frac{1}{4^2}-\frac{1}{2^2}\right) \\\\ & \mathrm{E}_{2 \rightarrow 4} \propto-\mathrm{R}\left(\frac{-3}{16}\right)=\frac{3 R}{16} \end{aligned} $$
(iii) Energy of excitation of electron from $n_1=2$ to $n_2=4$ is given as:
$$ \begin{aligned} \mathrm{E}_{2 \rightarrow 6} & \propto-\mathrm{R}\left(\frac{1}{n_2^2}-\frac{1}{n_1^2}\right) \\\\ \mathrm{E}_{2 \rightarrow 6} & \propto-R\left(\frac{1}{6^2}-\frac{1}{2^2}\right) \\\\ & =-\left(\frac{1}{36}-\frac{1}{4}\right) R \\\\ E_{2 \rightarrow 6} & \propto \frac{+8 R}{36} \end{aligned} $$
The ratio of the energy of transition in the two cases is given by :
$$ \begin{aligned} & \frac{E_{2 \rightarrow 4}}{E_{2 \rightarrow 6}}=\frac{3 R}{16} \times \frac{6}{8 R}=\frac{27}{32} \\\\ & E_{2 \rightarrow 4}=\frac{27}{32} \times E_{2 \rightarrow 6} \end{aligned} $$
the energy of transition from 2 to 4 excited state is $\frac{27}{32}$ times the energy of transition from 2 to 6 excited state.
$$ \psi_{n, l, m_l}=\frac{1}{\sqrt{\pi}}\left(\frac{Z}{a_0}\right)^{3 / 2} e^{-Z r / a_0} $$
Where, $\mathrm{Z}$ is atomic number of the element, $r$ is the variable distance of electron from the nucleus, $a_0$ is the Bohr's radius
For $1 \mathrm{~s}$ orbital, $n=1, l=0, m_l=0$ and wave function is represented as :
$$ \begin{aligned} & \psi_{1,0,0}=\frac{1}{\sqrt{\pi}}\left(\frac{Z}{a_0}\right)^{3 / 2} e^{-Z r / a_0} \\\\ \Rightarrow \psi_{1,0,0} & \propto\left(\frac{Z}{a_0}\right)^{3 / 2} e^{-Z r / a_0} \end{aligned} $$
(ii) Energy of excitation of electron from $n_1=2$ to $n_2=4$ is given as :
$$ \begin{aligned} & \mathrm{E}_{2 \rightarrow 4} \propto-\mathrm{R}\left(\frac{1}{n_2^2}-\frac{1}{n_1^2}\right) \\\\ & \mathrm{E}_{2 \rightarrow 4} \propto-\mathrm{R}\left(\frac{1}{4^2}-\frac{1}{2^2}\right) \\\\ & \mathrm{E}_{2 \rightarrow 4} \propto-\mathrm{R}\left(\frac{-3}{16}\right)=\frac{3 R}{16} \end{aligned} $$
(iii) Energy of excitation of electron from $n_1=2$ to $n_2=4$ is given as:
$$ \begin{aligned} \mathrm{E}_{2 \rightarrow 6} & \propto-\mathrm{R}\left(\frac{1}{n_2^2}-\frac{1}{n_1^2}\right) \\\\ \mathrm{E}_{2 \rightarrow 6} & \propto-R\left(\frac{1}{6^2}-\frac{1}{2^2}\right) \\\\ & =-\left(\frac{1}{36}-\frac{1}{4}\right) R \\\\ E_{2 \rightarrow 6} & \propto \frac{+8 R}{36} \end{aligned} $$
The ratio of the energy of transition in the two cases is given by :
$$ \begin{aligned} & \frac{E_{2 \rightarrow 4}}{E_{2 \rightarrow 6}}=\frac{3 R}{16} \times \frac{6}{8 R}=\frac{27}{32} \\\\ & E_{2 \rightarrow 4}=\frac{27}{32} \times E_{2 \rightarrow 6} \end{aligned} $$
the energy of transition from 2 to 4 excited state is $\frac{27}{32}$ times the energy of transition from 2 to 6 excited state.
Comments (0)