Sign In

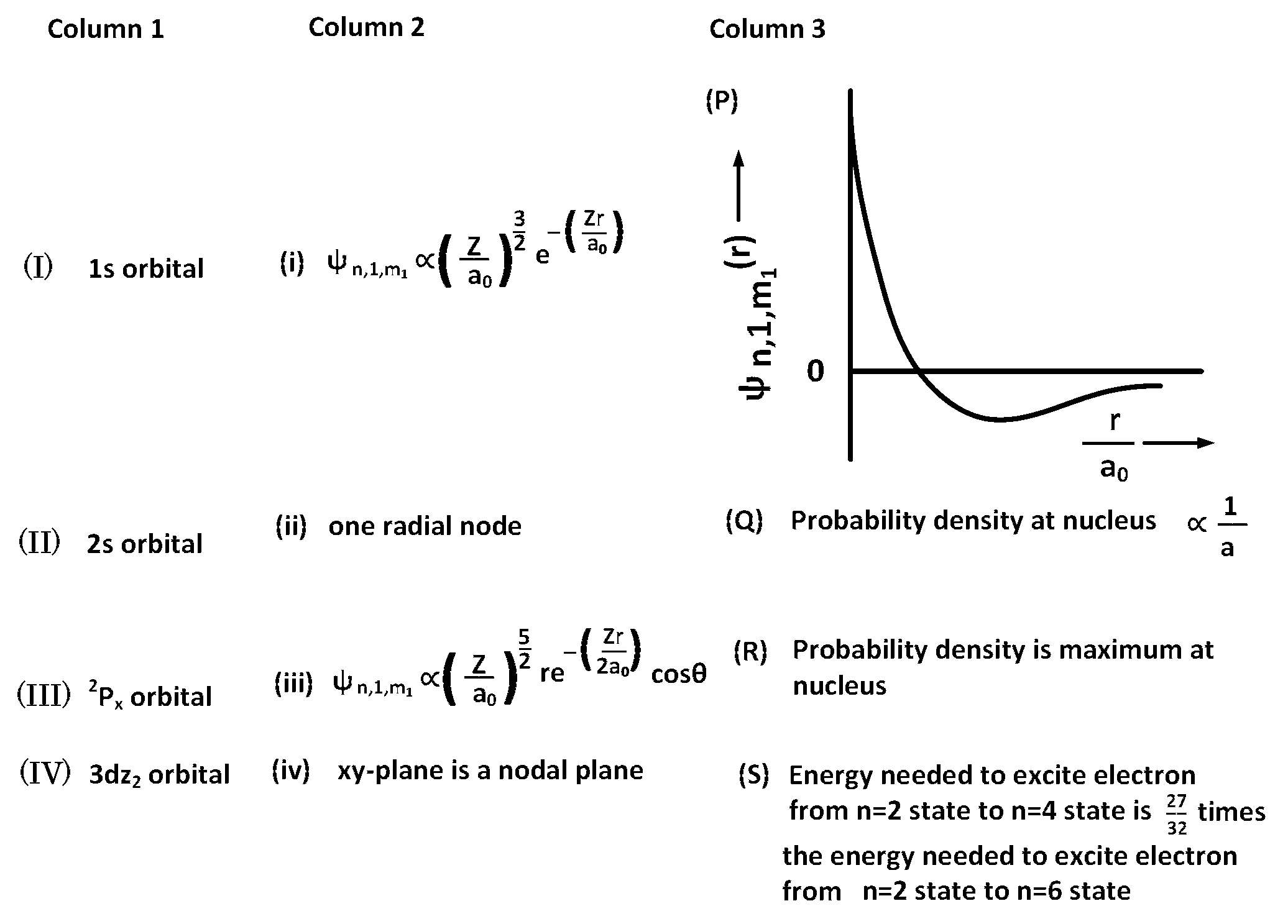
JEE Advance - Chemistry (2017 - Paper 1 Offline - No. 16)

The wave function, $${\psi _{n,1,{m_1}}}$$ is a mathematical function whose value depends upon spherical polar coordinates $$\left( {r,\theta ,\phi } \right)$$ of the electron and characterized by the quantum numbers $$n,1$$ and $${m_1}$$. Here $$r$$ is distance from nucleus, $$\theta $$ is colatitude and $$\phi $$ is azimuth. In the mathematical functions given in the table, $$Z$$ is atomic number and $${a_0}$$ is Bohr radius.

The wave function, $${\psi _{n,1,{m_1}}}$$ is a mathematical function whose value depends upon spherical polar coordinates $$\left( {r,\theta ,\phi } \right)$$ of the electron and characterized by the quantum numbers $$n,1$$ and $${m_1}$$. Here $$r$$ is distance from nucleus, $$\theta $$ is colatitude and $$\phi $$ is azimuth. In the mathematical functions given in the table, $$Z$$ is atomic number and $${a_0}$$ is Bohr radius.

The wave function, $${\psi _{n,1,{m_1}}}$$ is a mathematical function whose value depends upon spherical polar coordinates $$\left( {r,\theta ,\phi } \right)$$ of the electron and characterized by the quantum numbers $$n,1$$ and $${m_1}$$. Here $$r$$ is distance from nucleus, $$\theta $$ is colatitude and $$\phi $$ is azimuth. In the mathematical functions given in the table, $$Z$$ is atomic number and $${a_0}$$ is Bohr radius.

For $$H{e^ + }$$ ion, the only INCORRECT combination is
(I) (i) (R)
(II) (ii) (Q)
(I) (iii) (R)
(I) (i) (S)

Explanation

The ion $\mathrm{He}^{+}$having 1 electron (in $1 s$ orbital) is hydrogen like species; hence, its $1 s$ orbital will have:

(i) Wave function same as that of hydrogen, i.e.,

$$ \psi_{1,0,0}=\left(\frac{Z}{a_0}\right)^{3 / 2} e^{-Z r / a_0} $$

(ii) The probability density for the electron in the $1 s$ orbital is represented as:

JEE Advanced 2017 Paper 1 Offline Chemistry - Structure of Atom Question 10 English Explanation
For $1 s$ orbital probability density is maximum at the nucleus.

(iii) Probability density for $2 s$ orbitals is given by

$$ =\frac{1}{2 a_0^{3 / 2}}\left(1-\frac{r}{2 a_0}\right) e^{-r / 2 a_0} $$

Probability density $\propto \frac{1}{a_0^3}$

(iv) For electron in the $1 s$ orbital, the wave function of electron is not the function of angular wave function i.e., $\theta$ and $\phi$. Hence, 1 s orbital cannot have the wave function

$$ \psi_{n, l, m_l} \propto\left(\frac{Z}{a_0}\right)^{5 / 2} r e^{\left(-Z r / 2 a_0\right) \cos \theta} $$

Comments (0)

Advertisement