JEE Advance - Chemistry (2016 - Paper 2 Offline - No. 6)
Paragraph
Thermal decomposition of gaseous X2 to gaseous X at 298 K takes place according to the following equations:
X2 (g) $$\leftrightharpoons$$ 2X (g)
The standard reaction Gibbs energy, $$\Delta _rG^o$$, of this reaction is positive. At the start of the reaction, there is one mole of X2 and no X. As the reaction proceeds, the number of moles of X formed is given by $$\beta$$. Thus, $$\beta _{equilibrium}$$ is the number of moles of X formed at equilibrium. The reaction is carried out at a constant total pressure of 2 bar. Consider the gases to behave ideally. (Given R = 0.083 L bar K-1 mol-1)
Question
The equilibrium constant Kp for this reaction at 298 K, in terms of $$\beta _{equilibrium}$$, is
Thermal decomposition of gaseous X2 to gaseous X at 298 K takes place according to the following equations:
X2 (g) $$\leftrightharpoons$$ 2X (g)
The standard reaction Gibbs energy, $$\Delta _rG^o$$, of this reaction is positive. At the start of the reaction, there is one mole of X2 and no X. As the reaction proceeds, the number of moles of X formed is given by $$\beta$$. Thus, $$\beta _{equilibrium}$$ is the number of moles of X formed at equilibrium. The reaction is carried out at a constant total pressure of 2 bar. Consider the gases to behave ideally. (Given R = 0.083 L bar K-1 mol-1)
Question
The equilibrium constant Kp for this reaction at 298 K, in terms of $$\beta _{equilibrium}$$, is
$${{8\beta _{equilibrium}^2} \over {2 - {\beta _{equilibrium}}}}$$
$${{8\beta _{equilibrium}^2} \over {4 - {\beta _{equilibrium}^2}}}$$
$${{4\beta _{equilibrium}^2} \over {2 - {\beta _{equilibrium}}}}$$
$${{4\beta _{equilibrium}^2} \over {4 - {\beta _{equilibrium}^2}}}$$
Explanation
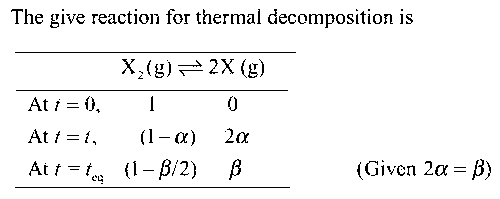
Total number of moles at equilibrium = (1 + $$\alpha$$) = 1 + (beq / 2)
Therefore,
$${p_x} = \left( {{{{\beta _{eq}}} \over {1 + ({\beta _{eq}}/2)}}{p_T}} \right)$$
$${p_{{x_2}}} = \left( {{{1 - ({\beta _{eq}}/2)} \over {1 + ({\beta _{eq}}/2)}}{p_T}} \right)$$
Therefore, the equilibrium constant Kp is given by
$${K_p} = {{p_x^2} \over {{p_{{x_2}}}}} = {{\left( {{{{\beta _{eq}}} \over {1 + ({\beta _{eq}}/2)}}{p_T}} \right)} \over {\left( {{{1 - ({\beta _{eq}}/2)} \over {1 + ({\beta _{eq}}/2)}}{p_T}} \right)}}$$
$$ = {{\beta _{eq}^2} \over {1 - (\beta _{eq}^2/4)}}{p_T} = {{\beta _{eq}^2} \over {1 - (\beta _{eq}^2/4)}} \times 2 = {{8\beta _{eq}^2} \over {4 - \beta _{eq}^2}}$$
Comments (0)


