JEE Advance - Chemistry (2016 - Paper 1 Offline - No. 7)
P is the probability of finding the 1s electron of hydrogen atom in a spherical shell of infinitesimal thickness, dr, at a distance r from the nucleus. The volume of this shell is $$4\pi r^2dr$$. The quantitative ketch of the dependence of P on r is
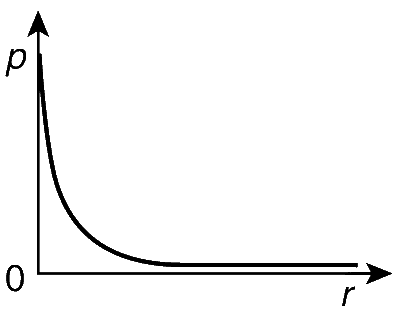
Explanation
The probability of finding an electron of hydrogen atom in a spherical shell of infinitesimal thickness, $d r$, at a distance $r$ from the nucleus, with volume $d V=4 \pi r^2 d r$ is
$$ P=\psi^2 \cdot d V=\psi^2 \cdot 4 \pi r^2 d r=R^2(r) 4 \pi r^2 d r $$
Here, $R^2(r)$ is the radial density function.
For $1 s$ subshell, $n=1, l=0$ and $n-l-1=0$. Thus, the number of radial and angular nodes $=0$. For 1s orbital, the probability of finding an electron will be maximum at near to the the nucleus, as 1s orbital is the nearest to the nucleus as it is the lowest orbital in terms of energy. Therefore, the plot of radial probability $P=R^2(r) 4 \pi r^2$ versus $r$ is as follows :

$$ P=\psi^2 \cdot d V=\psi^2 \cdot 4 \pi r^2 d r=R^2(r) 4 \pi r^2 d r $$
Here, $R^2(r)$ is the radial density function.
For $1 s$ subshell, $n=1, l=0$ and $n-l-1=0$. Thus, the number of radial and angular nodes $=0$. For 1s orbital, the probability of finding an electron will be maximum at near to the the nucleus, as 1s orbital is the nearest to the nucleus as it is the lowest orbital in terms of energy. Therefore, the plot of radial probability $P=R^2(r) 4 \pi r^2$ versus $r$ is as follows :

Comments (0)


