JEE Advance - Chemistry (2015 - Paper 2 Offline - No. 18)
One mole of a monoatomic real gas satisfies the equation p(V $$-$$ b) = RT where b is a constant. The relationship of interatomic potential V(r) and interatomic distance r for the gas is given by
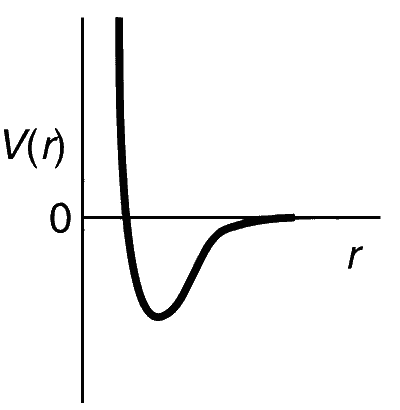
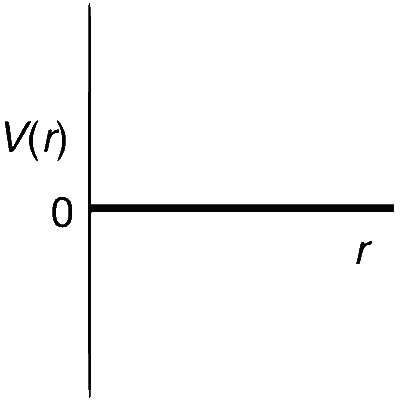
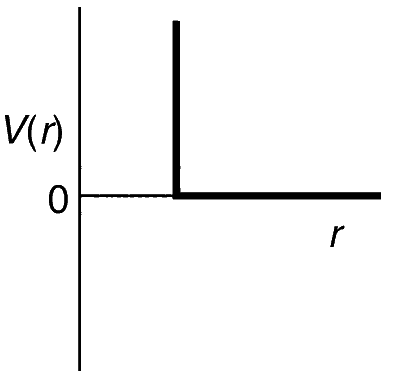
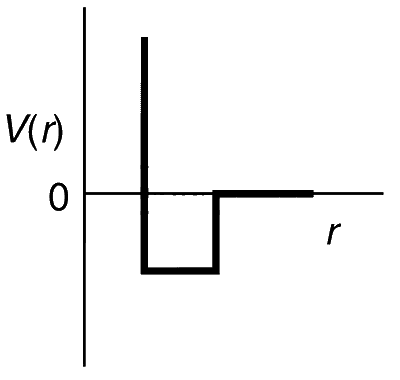
Explanation
The given equation is $\mathrm{P}(\mathrm{V}-b)=\mathrm{RT}$,
On comparing with van Der Waal's equation
$$ \left[\mathrm{P}+\frac{a}{\mathrm{~V}^2}\right][\mathrm{V}-b]=\mathrm{RT} \text { we get } a=0 $$
Hence, only repulsive forces are present which are contributive only at very close distance.
Thus, the potential energy will increase abruptly, so graph (c) is correct. The dominance of repulsive force can be shown by using the compressibility factor.
$$ \begin{aligned} \mathrm{P}(\mathrm{V}-b) & =\mathrm{RT} \\\\ \mathrm{PV} & =\mathrm{Pb}+\mathrm{RT} \\\\ \frac{\mathrm{PV}}{\mathrm{RT}} & =\frac{\mathrm{Pb}}{\mathrm{RT}}+1 \end{aligned} $$
$$ Z=\frac{P b}{\mathrm{RT}}+1 \text {, i.e., } \mathrm{Z}>1 \text { (Repulsive forces) } $$
On comparing with van Der Waal's equation
$$ \left[\mathrm{P}+\frac{a}{\mathrm{~V}^2}\right][\mathrm{V}-b]=\mathrm{RT} \text { we get } a=0 $$
Hence, only repulsive forces are present which are contributive only at very close distance.
Thus, the potential energy will increase abruptly, so graph (c) is correct. The dominance of repulsive force can be shown by using the compressibility factor.
$$ \begin{aligned} \mathrm{P}(\mathrm{V}-b) & =\mathrm{RT} \\\\ \mathrm{PV} & =\mathrm{Pb}+\mathrm{RT} \\\\ \frac{\mathrm{PV}}{\mathrm{RT}} & =\frac{\mathrm{Pb}}{\mathrm{RT}}+1 \end{aligned} $$
$$ Z=\frac{P b}{\mathrm{RT}}+1 \text {, i.e., } \mathrm{Z}>1 \text { (Repulsive forces) } $$
Comments (0)


