Sign In

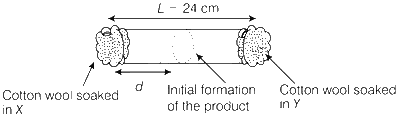
JEE Advance - Chemistry (2014 - Paper 2 Offline - No. 11)

X and Y are two volatile liquids with molar weights of 10 g mol$$-$$1 and 40 g mol$$-$$1, respectively. Two cotton plugs, one soaked in X and the other soaked in Y, are simultaneously placed at the ends of a tube of length L = 24 cm, as shown in the figure. The tube is filled with an inert gas at 1 atmosphere pressure and a temperature of 300 K. Vapours of X and Y react to form a product which is first observed at a distance d cm from the plug soaked in X. Take X and Y to have equal molecular diameters and assume ideal behaviour for the inert gas and the two vapours.

X and Y are two volatile liquids with molar weights of 10 g mol$$-$$1 and 40 g mol$$-$$1, respectively. Two cotton plugs, one soaked in X and the other soaked in Y, are simultaneously placed at the ends of a tube of length L = 24 cm, as shown in the figure. The tube is filled with an inert gas at 1 atmosphere pressure and a temperature of 300 K. Vapours of X and Y react to form a product which is first observed at a distance d cm from the plug soaked in X. Take X and Y to have equal molecular diameters and assume ideal behaviour for the inert gas and the two vapours.

X and Y are two volatile liquids with molar weights of 10 g mol$$-$$1 and 40 g mol$$-$$1, respectively. Two cotton plugs, one soaked in X and the other soaked in Y, are simultaneously placed at the ends of a tube of length L = 24 cm, as shown in the figure. The tube is filled with an inert gas at 1 atmosphere pressure and a temperature of 300 K. Vapours of X and Y react to form a product which is first observed at a distance d cm from the plug soaked in X. Take X and Y to have equal molecular diameters and assume ideal behaviour for the inert gas and the two vapours.

The value of d in cm (shown in the figure), as estimated from Graham's law, is
8
12
16
20

Explanation

Using Graham's law of diffusion, we have that for identical conditions, rate of diffusion varies inversely with square root of mass of the gases. So,

$${x \over {24 - x}} = {\left( {{{40} \over {10}}} \right)^{1/2}} \Rightarrow x = 16$$

Comments (0)

Advertisement