(i) The solubility of $\mathrm{AgCl}(\mathrm{s})$ in saturated solution is expressed as :

$$ \mathrm{H}_2 \mathrm{O}+\mathrm{AgCl}_{(s)} \rightarrow \underset{x}{\mathrm{Ag}^{+}}(a q)+\underset{x} {\mathrm{Cl}^{-}}(a q) $$

Though $\mathrm{AgCl}(\mathrm{s})$ has low solubility with $\mathrm{K}_{s p}=1.6$ $\times 10^{-10}$ still some silver $\left(\mathrm{Ag}^{+}\right)$and chloride $\left(\mathrm{Cl}^{-}\right)$ are dissolved in solution. Let the concentration of these ions be $x \mathrm{~mol}^{-1}$ (in solution).

$$ \begin{aligned} {[\mathrm{Ag}]^{+} } & =\left[\mathrm{Cl}^{-}\right]=x \\ & =1.6 \times 10^{-10} \\ \mathrm{CuCl}(s)+\mathrm{H}_2 \mathrm{O}(l) & \rightleftharpoons \mathrm{Cu}^{+}(a q)+\mathrm{Cl}^{-}(a q) \end{aligned} $$

(ii) Similarly though CuCl has low solubility in aqueous solution $\left[K_{s p}=1.0 \times 10^{-6}\right]$, still some copper $\left(\mathrm{Cu}^{+}\right)$and chloride $\left(\mathrm{Cl}^{-}\right)$are dissolved in the solution. Let the concentration of these ions be $y \mathrm{~mol} \mathrm{~L}^{-1}$ (in solution).

$$ \left[\mathrm{Cu}^{+}\right]=\left[\mathrm{Cl}^{-}\right]=y $$

(iii) The salts $\mathrm{AgCl}(\mathrm{s})$ and $\mathrm{CuCl}(\mathrm{s})$ are present in equilibrium with their ions as follows :

$\text{AgCl}(s) + \text{H}_2\text{O} \rightleftharpoons \underset{x}{\text{Ag}^+ (aq)} + \underset{x+y}{\text{Cl}^- (aq)}$

$K_{sp}(\text{AgCl}) = 1.6 \times 10^{-10} = x(x + y) \quad \ldots \text{(i)}$

$\text{CuCl}_{(s)} + \text{H}_2\text{O} \rightleftharpoons \underset{x}{\text{Cu}^+ (aq)} + \underset{y+x}{\text{Cl}^- (aq)}$

$K_{sp}(\text{CuCl}) = 1.0 \times 10^{-6} = y \times (x + y) \quad \ldots \text{(ii)}$

Dividing equation (ii) by (i) :

$ \frac{1.0 \times 10^{-6}}{1.6 \times 10^{-10}} = \frac{y}{x} $

$ \frac{y}{x} = \frac{1.0}{1.6} \times 10^4 $ …(iii)

No. of moles of CuCl = $0.1 \text{ mol}$

Volume of solution = $1 \text{ L}$

$\begin{aligned} & \text { Concentration of } \mathrm{CuCl}=\frac{\text { No. of moles of } \mathrm{CuCl}}{\text { Volume of solution }} \\\\ & \text { Concentration of } \mathrm{CuCl}=\frac{0.1 \mathrm{~mol}}{1 \mathrm{~L}}=0.1\end{aligned}$

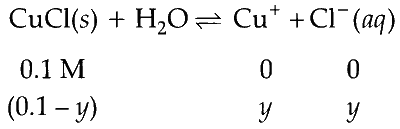
$\begin{aligned} \mathrm{K}_{s p} & =1.0 \times 10^{-6}=y \times y \\\\ y & =\sqrt{10^{-6}}=10^{-3} \mathrm{~mol} \mathrm{~L}^{-1}\end{aligned}$

Substituting value of $y$ in equation (iii),

$$ \begin{aligned} \frac{\left[\mathrm{Cu}^{+}\right]}{\left[\mathrm{Ag}^{+}\right]}=\frac{y}{x} & =\frac{10^{-3} \mathrm{~mol} \mathrm{~L}^{-1}}{x}=10^4 \frac{1.0}{1.6} \\ x & =1.6 \times 10^{-7} \end{aligned} $$

The concentration of silver ion, $\left[\mathrm{Ag}^{+}\right]=x$ $=1.6 \times 10^{-7} \mathrm{~mol}$ L.

Hence, the value of $x$ in 1.6 $\times 10^{-x}$ is 7 .