JEE Advance - Chemistry (2010 - Paper 2 Offline - No. 13)
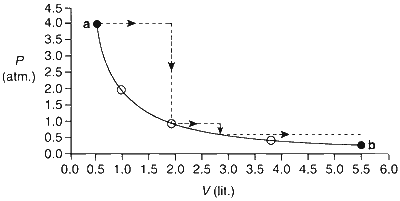
One mole of an ideal gas is taken from $\mathbf{a}$ to $\mathbf{b}$ along two paths denoted by the solid and the dashed lines as shown in the graph below. If the work done along the solid line path is $W_{\text {s }}$ and that dotted line path is $W_{\mathrm{d}}$, then the integer closest to the ratio $W_{\mathrm{d}} / W_{\mathrm{s}}$ is
Answer
2
Explanation
For calculating work done, we need to calculate the area under curve for solid and dotted lines.
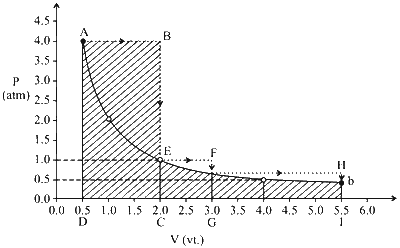
Let ' $w_d$ and ' $w$ ' be work done along the dotted and solid path respectively.
$$ \begin{aligned} & \mathrm{W}_d=\text { Area ABCD }+ \text { Area EFGC + Area FGIH } \\\\ & w_d =4 \times 1.5+1 \times 1+2.5 \times 2 / 3 \\\\ & =8.65 \end{aligned} $$
$$ \begin{aligned} &\text { Process of work done }\left(w_s\right) \text { is isothermal }\\\\ &\begin{aligned} w_s & =2 \times 2.303 \log \frac{5.5}{0.5} \\\\ & =2 \times 2.303 \times \log 11 \\\\ & =2 \times 2.303 \times 1.0414=4.79 \\\\ \frac{w_d}{w_s} & =\frac{8.65}{4.79}=1.80 \simeq 2 \end{aligned} \end{aligned} $$Comments (0)


