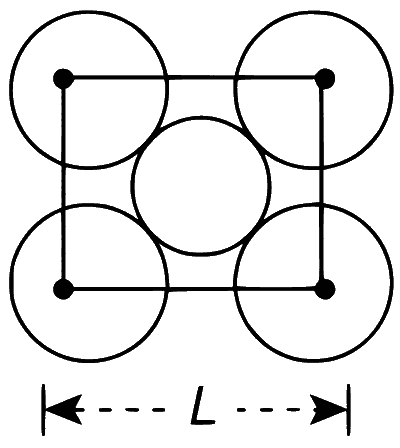
The diagonal is given as 4r, where r is the radius of atom or sphere forming close packed structure.

$$ \begin{aligned} \text { Diagonal } & =\sqrt{\mathrm{L}^2+\mathrm{L}^2}=\sqrt{2 \mathrm{~L}^2} \\\\ 4 r & =\sqrt{2 \mathrm{~L}^2} \text { or } \mathrm{L}=\frac{4 r}{\sqrt{2}}=2 \sqrt{2} r \\\\ \text { or } \text { Total area } & =\mathrm{L}^2 \\\\ (2 \sqrt{2} r)^2 & =8 r^2 \end{aligned} $$

Number of spheres inside the square is

$$ 1+4\left(\frac{1}{4}\right)=2 $$

Area of each sphere $=\pi r^2$

Total area of spheres $=2 \times \pi r^2$

$$ \begin{aligned} \text { Packing fraction } & =\frac{\text { Total area of spheres }}{\text { Total area }} \\\\ & =\frac{2 \times \pi r^2}{8 r^2}=\frac{\pi}{4}=0.785 \end{aligned} $$

So, the percentage fraction is $78.5 \%$.