JEE Advance - Chemistry (2009 - Paper 2 Offline - No. 15)
The total number of $$\alpha$$ and $$\beta$$ particles emitted in the nuclear reaction $$_{92}^{238}U \to _{82}^{214}Pb$$ is _________.
Answer
8
Explanation
The equation for the nuclear fission reaction is:
$$ { }_{92}^{238} \mathrm{U} \longrightarrow{ }_{82}^{214} \mathrm{~Pb} $$
It is also written as
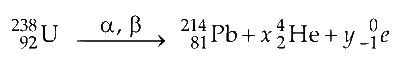
So, to find the alpha particle you can solve it by atomic mass of $\mathrm{Pb}$
$$ =\text { Atomic mass of } \mathrm{U}-4 a $$
Atomic mass of $U=238$
Atomic mass of $\mathrm{Pb}=214$
So, by putting the values in equation (i), you will get
$$ 206=238-4 a $$
$$ \begin{aligned} \therefore \alpha & =\frac{238-214}{4} =6 \end{aligned} $$
Now, find the beta particle by using formula
Atomic number of $\mathrm{U}=$ Atomic number of $\mathrm{Pb}+2 \alpha+\beta$.
Where, atomic no. of $U$ is 92 and atomic no. of $\mathrm{Pb}$ is 82 and the value of $\alpha$ that we have find is 6. By putting the values you will get.
$$ 92=82+2 \times 6=\beta $$
Therefore, $ \beta=92-94=2$
Thus, the number of alpha and beta particles is 6 and 2.
$$ { }_{92}^{238} \mathrm{U} \longrightarrow{ }_{82}^{214} \mathrm{~Pb} $$
It is also written as
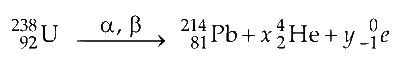
So, to find the alpha particle you can solve it by atomic mass of $\mathrm{Pb}$
$$ =\text { Atomic mass of } \mathrm{U}-4 a $$
Atomic mass of $U=238$
Atomic mass of $\mathrm{Pb}=214$
So, by putting the values in equation (i), you will get
$$ 206=238-4 a $$
$$ \begin{aligned} \therefore \alpha & =\frac{238-214}{4} =6 \end{aligned} $$
Now, find the beta particle by using formula
Atomic number of $\mathrm{U}=$ Atomic number of $\mathrm{Pb}+2 \alpha+\beta$.
Where, atomic no. of $U$ is 92 and atomic no. of $\mathrm{Pb}$ is 82 and the value of $\alpha$ that we have find is 6. By putting the values you will get.
$$ 92=82+2 \times 6=\beta $$
Therefore, $ \beta=92-94=2$
Thus, the number of alpha and beta particles is 6 and 2.
Comments (0)


