Given reaction : 2N₂O₅(g) $$\to$$ 4NO₂(g) + O₂(g)

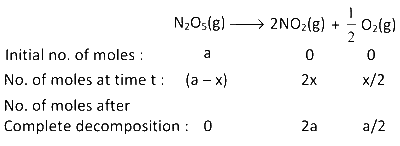
$$\therefore$$ Total no. of moles at time, $$t = a - x + 2x + {x \over 2} = a + {3 \over 2}x$$

Total no. of moles after complete decomposition

$$ = 2a + {a \over 2} = {5 \over 2}a$$

At a given volume and temperature, P $$\propto$$ n [Assuming ideal behaviour of gas mixture]

According to the given data, $${5 \over 2}$a $$\propto$$ 584.5 mm Hg ...... [1]

and $$a + {3 \over 2}x \propto 284.5$$ mm Hg ............... [2]

$$\therefore$$ a $$\propto$$ 233.8 mm Hg and $${3 \over 2}x \propto 284.5-a$$

or, $${3 \over 2}x \propto 284.5 - 233.8 \propto 50.7$$ mm Hg

$$\therefore$$ x $$\propto$$ 33.8 mm Hg

Therefore, (a $$-$$ x) $$\propto$$ (233.8 $$-$$ 33.8) mm Hg

i.e., (a $$-$$ x) $$\propto$$ 200 mm Hg

$$\therefore$$ $$k = {{2.303} \over t}\log {a \over {a - x}} = {{2.303} \over {30}}\log {{233.8} \over {200}}$$

or, k = 5.21 $$\times$$ 10^$$-$$3 min^$$-$$1