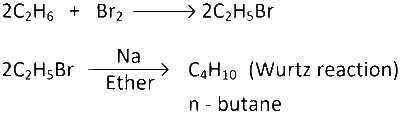
Now, assume moles of $${C_2}{H_6} = x$$

$$\therefore$$ Moles of $${C_2}{H_5}Br = x$$ when 100% yield.

Given that 90% yield of $${C_2}{H_5}Br$$ happens.

$$\therefore$$ Moles of $${C_2}{H_5}Br = x \times {{90} \over {100}} = 0.9x$$

Now, from 2 moles of $${C_2}{H_5}Br$$ 1 mole of $${C_4}{H_{10}}$$ produced.

$$\therefore$$ From 0.9x moles of $${C_2}{H_5}Br$$ $${1 \over 2} \times 0.9x$$ moles of $${C_4}{H_{10}}$$ produced when 100% yield happens. But given that 85% yield of $${C_4}{H_{10}}$$ happens.

$$\therefore$$ Moles of $${C_4}{H_{10}} = {1 \over 2} \times 0.9x \times {{85} \over {100}}$$

$$ = {{(0.9 \times 0.85)x} \over 2}$$

According to question,

$${{(0.9 \times 0.85)x} \over 2} = {{55} \over {58}}$$

$$ \Rightarrow x = {{55} \over {29 \times 0.9 \times 0.85}} = 2.48$$

$$\therefore$$ Volume of $${C_2}{H_6} = 2.48 \times 22.4$$ Litres

$$ = 55.552$$ Litres