JEE MAIN - Physics (2012 - No. 19)
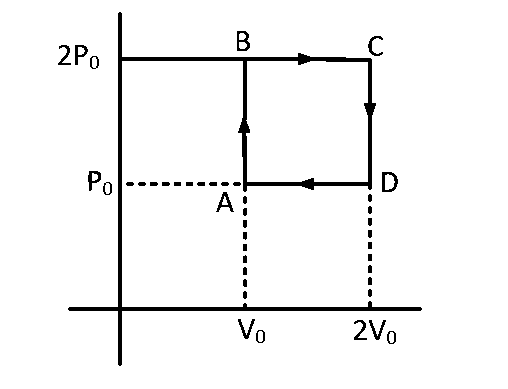
Helium gas goes through a cycle $$ABCD$$ (consisting of two isochoric and isobaric lines) as shown in figure efficiency of this cycle is nearly : (Assume the gas to be close to ideal gas)

$$15.4\% $$
$$9.1\% $$
$$10.5\% $$
$$12.5\% $$
Explanation
Heat given to system $$ = {\left( {n{C_v}\Delta T} \right)_{A \to B}} + {\left( {n{C_p}\Delta T} \right)_{B \to C}}$$
$$ = {\left[ {{3 \over 2}\left( {nR\Delta T} \right)} \right]_{A \to B}} + {\left[ {{5 \over 2}\left( {nR\Delta T} \right)} \right]_{B \to C}}$$
$$ = {\left[ {{3 \over 2} \times {V_0}\Delta P} \right]_{A \to B}} + {\left[ {{5 \over 2} \times 2{P_0} \times {V_0}} \right]_{B \to C}}$$
$$ = {{13} \over 2}{P_0}{V_0}$$
and $${W_0} = {P_0}{V_0}$$
$$\eta = {{Work} \over {heat\,\,given}}$$
$$ = {{{P_0}{V_0}} \over {{{13} \over 2}{P_0}{V_0}}} \times 100$$
$$ = 15.4\% $$
$$ = {\left[ {{3 \over 2}\left( {nR\Delta T} \right)} \right]_{A \to B}} + {\left[ {{5 \over 2}\left( {nR\Delta T} \right)} \right]_{B \to C}}$$
$$ = {\left[ {{3 \over 2} \times {V_0}\Delta P} \right]_{A \to B}} + {\left[ {{5 \over 2} \times 2{P_0} \times {V_0}} \right]_{B \to C}}$$
$$ = {{13} \over 2}{P_0}{V_0}$$
and $${W_0} = {P_0}{V_0}$$
$$\eta = {{Work} \over {heat\,\,given}}$$
$$ = {{{P_0}{V_0}} \over {{{13} \over 2}{P_0}{V_0}}} \times 100$$
$$ = 15.4\% $$
Comments (0)


