JEE MAIN - Physics (2012 - No. 11)
A particle of mass $$m$$ is at rest at the origin at time $$t=0.$$ It is subjected to a force $$F\left( t \right) = {F_0}{e^{ - bt}}$$ in the $$x$$ direction. Its speed $$v(t)$$ is depicted by which of the following curves?
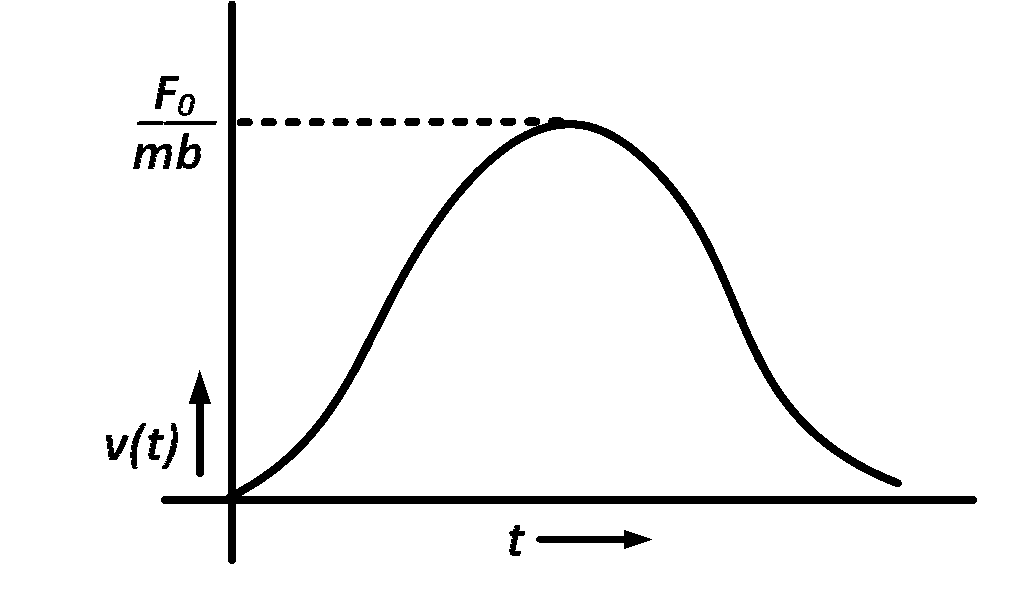
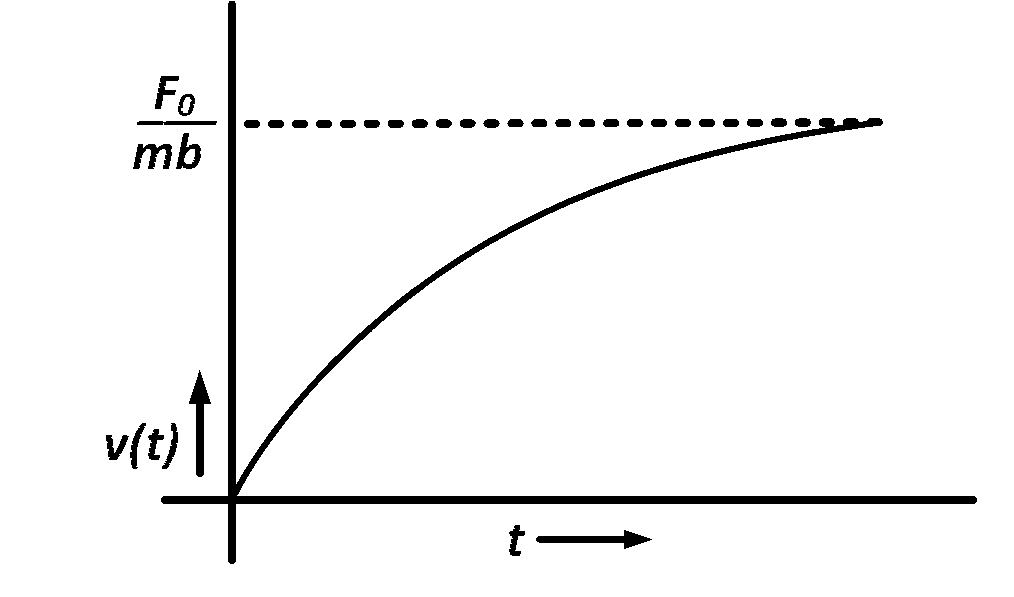
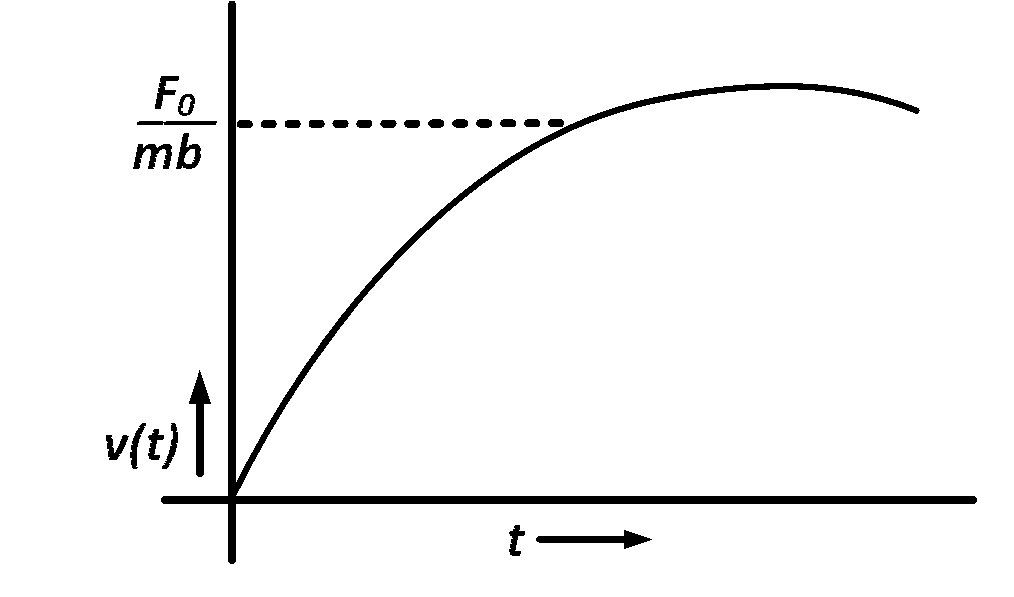
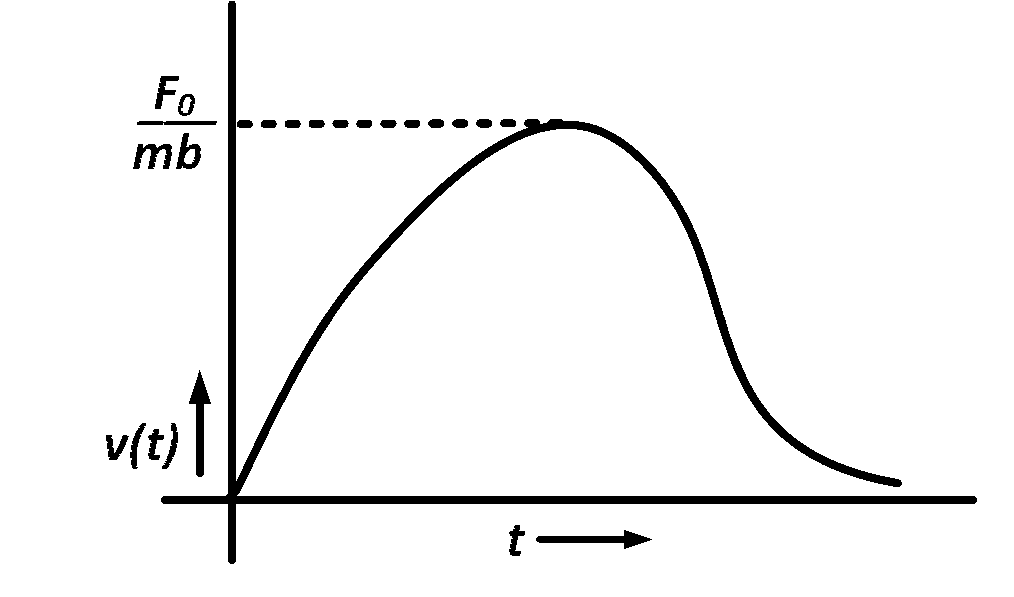
Explanation
Given that $$F\left( t \right) = {F_0}{e^{ - bt}} $$
$$\Rightarrow m{{dv} \over {dt}} = {F_0}{e^{ - bt}}$$
$${{dv} \over {dt}} = {{{F_0}} \over m}{e^{ - bt}} $$
$$\Rightarrow \int\limits_0^v {dv} = {{{F_0}} \over m}\int\limits_0^t {{e^{ - bt}}} \,dt$$
$$v = {{{F_0}} \over m}\left[ {{{{e^{ - bt}}} \over { - b}}} \right]_0^t = {{{F_0}} \over {mb}}\left[ { - \left( {{e^{ - bt}} - {e^{ - 0}}} \right)} \right]$$
$$ \Rightarrow v = {{{F_0}} \over {mb}}\left[ {1 - {e^{ - bt}}} \right]$$
$$ \Rightarrow v_{max} = {{{F_0}} \over {mb}}$$
$$\Rightarrow m{{dv} \over {dt}} = {F_0}{e^{ - bt}}$$
$${{dv} \over {dt}} = {{{F_0}} \over m}{e^{ - bt}} $$
$$\Rightarrow \int\limits_0^v {dv} = {{{F_0}} \over m}\int\limits_0^t {{e^{ - bt}}} \,dt$$
$$v = {{{F_0}} \over m}\left[ {{{{e^{ - bt}}} \over { - b}}} \right]_0^t = {{{F_0}} \over {mb}}\left[ { - \left( {{e^{ - bt}} - {e^{ - 0}}} \right)} \right]$$
$$ \Rightarrow v = {{{F_0}} \over {mb}}\left[ {1 - {e^{ - bt}}} \right]$$
$$ \Rightarrow v_{max} = {{{F_0}} \over {mb}}$$
Comments (0)


