JEE MAIN - Physics (2011 - No. 9)
A current $$I$$ flows in an infinitely long wire with cross section in the form of a semi-circular ring of radius $$R.$$ The magnitude of the magnetic induction along its axis is:
$${{{\mu _0}I} \over {2{\pi ^2}R}}$$
$${{{\mu _0}I} \over {2\pi R}}$$
$${{{\mu _0}I} \over {4\pi R}}$$
$${{{\mu _0}I} \over {{\pi ^2}R}}$$
Explanation
Current in a small element, $$dl = {{d\theta } \over \pi }I$$
Magnetic field due to the element
$$dB = {{{\mu _0}} \over {4\pi }}{{2dl} \over R}$$
The component $$dB$$ $$\cos \,\theta ,$$ of the field is canceled by another opposite component.
Therefore,
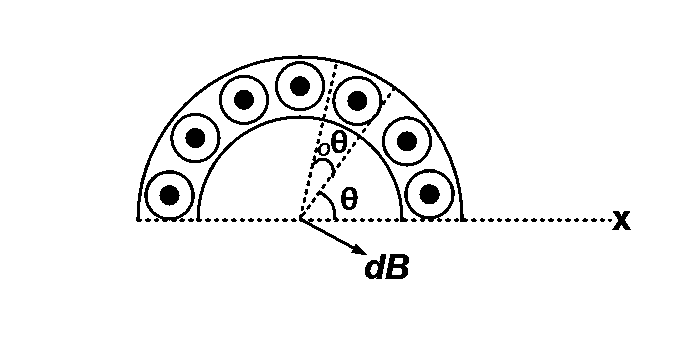
$${B_{net}} = \int {dB\sin \theta = {{{\mu _0}I} \over {2{\pi ^2}{R_0}}}} $$
$$\int\limits_0^\pi {\sin \theta d\theta = {{{\mu _0}I} \over {{\pi ^2}R}}} $$
Magnetic field due to the element
$$dB = {{{\mu _0}} \over {4\pi }}{{2dl} \over R}$$
The component $$dB$$ $$\cos \,\theta ,$$ of the field is canceled by another opposite component.
Therefore,

$${B_{net}} = \int {dB\sin \theta = {{{\mu _0}I} \over {2{\pi ^2}{R_0}}}} $$
$$\int\limits_0^\pi {\sin \theta d\theta = {{{\mu _0}I} \over {{\pi ^2}R}}} $$
Comments (0)


