JEE MAIN - Physics (2011 - No. 5)
Let $$x$$-$$z$$ plane be the boundary between two transparent media. Medium $$1$$ in $$z \ge 0$$ has a refractive index of $$\sqrt 2 $$ and medium $$2$$ with $$z < 0$$ has a refractive index of $$\sqrt 3 .$$ A ray of light in medium $$1$$ given by the vector $$\overrightarrow A = 6\sqrt 3 \widehat i + 8\sqrt 3 \widehat j - 10\widehat k$$ is incident on the plane of separation. The angle of refraction in medium $$2$$ is:
$${45^ \circ }$$
$${60^ \circ }$$
$${75^ \circ }$$
$${30^ \circ }$$
Explanation
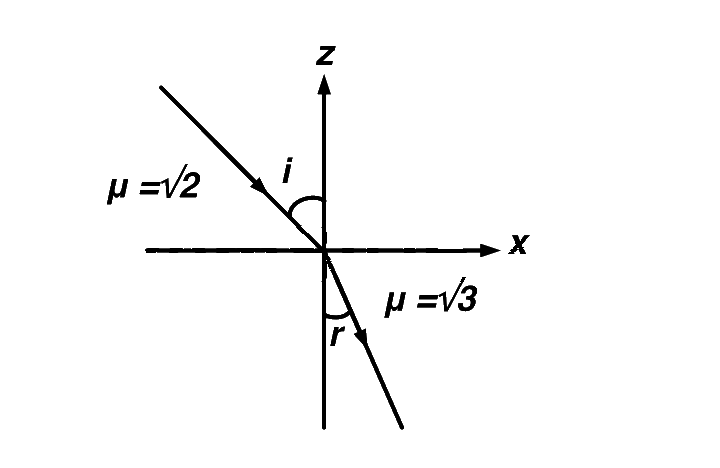
Angle of incidence is given by
$$\cos \left( {\pi - i} \right) = {{\left( {6\sqrt 3 \widehat i + 8\sqrt 3 \widehat j - 10\widehat k} \right).\widehat k} \over {20}}$$
$$ - \cos \,i = - {1 \over 2}$$
$$\angle i = {60^ \circ }$$
From Snell's law, $$\sqrt 2 \sin i = \sqrt 3 \sin r$$
$$ \Rightarrow $$ $$\angle r = {45^ \circ }$$
Comments (0)


