JEE MAIN - Physics (2011 - No. 23)
A mass $$m$$ hangs with the help of a string wrapped around a pulley on a frictionless bearing. The pulley has mass $$m$$ and radius $$R.$$ Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass $$m,$$ if the string does not slip on the pulley, is:
$$g$$
$${2 \over 3}g$$
$${g \over 3}$$
$${3 \over 2}g$$
Explanation
This is the free body diagram of pulley and mass
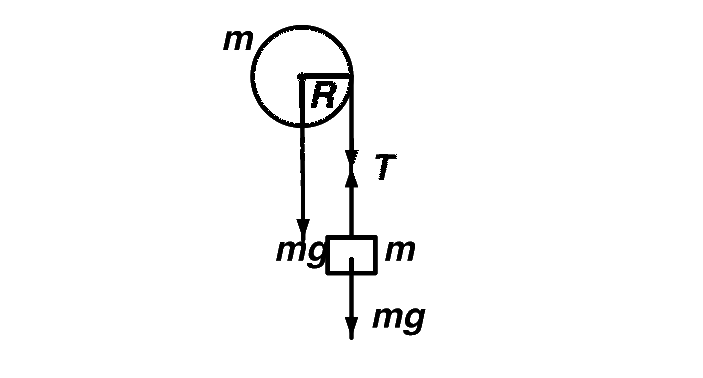
For translation motion of the block,
$$mg - T = ma\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.....\left( 1 \right)$$
For rotational motion of the pulley,
$$T\times R = I\alpha = I{a \over R}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( 2 \right)$$
where $$\alpha = $$ angular acceleration of disc = $$ {a \over R}$$
and $$I = {1 \over 2}m{R^2}$$ (For circular disc)
Solving $$(1)$$ & $$(2),$$
$$a = {{mg} \over {\left( {m + {I \over {{R^2}}}} \right)}} = {{mg} \over {m + {{m{R^2}} \over {2{R^2}}}}}$$
$$ = {{2mg} \over {3m}} = {{2g} \over 3}$$

For translation motion of the block,
$$mg - T = ma\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,.....\left( 1 \right)$$
For rotational motion of the pulley,
$$T\times R = I\alpha = I{a \over R}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( 2 \right)$$
where $$\alpha = $$ angular acceleration of disc = $$ {a \over R}$$
and $$I = {1 \over 2}m{R^2}$$ (For circular disc)
Solving $$(1)$$ & $$(2),$$
$$a = {{mg} \over {\left( {m + {I \over {{R^2}}}} \right)}} = {{mg} \over {m + {{m{R^2}} \over {2{R^2}}}}}$$
$$ = {{2mg} \over {3m}} = {{2g} \over 3}$$
Comments (0)


