JEE MAIN - Physics (2011 - No. 21)
Two bodies of masses $$m$$ and $$4$$ $$m$$ are placed at a distance $$r.$$ The gravitational potential at a point on the line joining them where the gravitational field is zero is:
$$ - {{4Gm} \over r}$$
$$ - {{6Gm} \over r}$$
$$ - {{9Gm} \over r}$$
zero
Explanation
Let the gravitational field at $$P,$$ distant $$x$$ from mass $$m,$$ be zero.
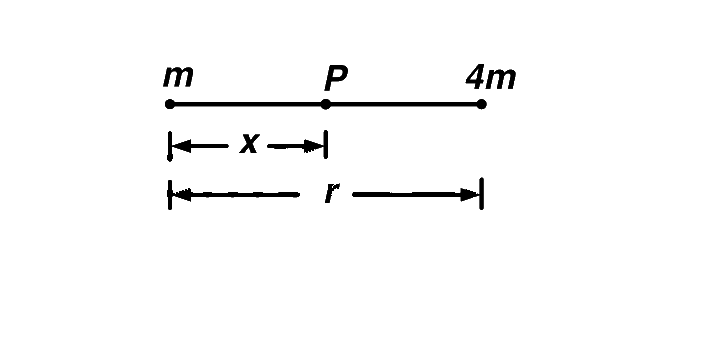
$$\therefore$$ $${{Gm} \over {{x^2}}} = {{4Gm} \over {{{\left( {r - x} \right)}^2}}}$$
$$ \Rightarrow 4{x^2} = {\left( {r - x} \right)^2}$$
$$ \Rightarrow 2x = r - x$$
$$ \Rightarrow x = {r \over 3}$$
Gravitational potential at point $$P,$$
$$V = - {{Gm} \over {{r \over 3}}} - {{4Gm} \over {{{2r} \over 3}}} = -{{9Gm} \over r}$$

$$\therefore$$ $${{Gm} \over {{x^2}}} = {{4Gm} \over {{{\left( {r - x} \right)}^2}}}$$
$$ \Rightarrow 4{x^2} = {\left( {r - x} \right)^2}$$
$$ \Rightarrow 2x = r - x$$
$$ \Rightarrow x = {r \over 3}$$
Gravitational potential at point $$P,$$
$$V = - {{Gm} \over {{r \over 3}}} - {{4Gm} \over {{{2r} \over 3}}} = -{{9Gm} \over r}$$
Comments (0)


