JEE MAIN - Physics (2011 - No. 11)
Two identical charged spheres suspended from a common point by two massless strings of length $$l$$ are initially a distance $$d\left( {d < < 1} \right)$$ apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate. As a result charges approach each other with a velocity $$v$$. Then as a function of distance $$x$$ between them,
$$v\, \propto \,{x^{ - 1}}$$
$$y\, \propto \,{x^{{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}}}$$
$$v\, \propto \,x$$
$$v\, \propto \,{x^{ - {\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}}}$$
Explanation
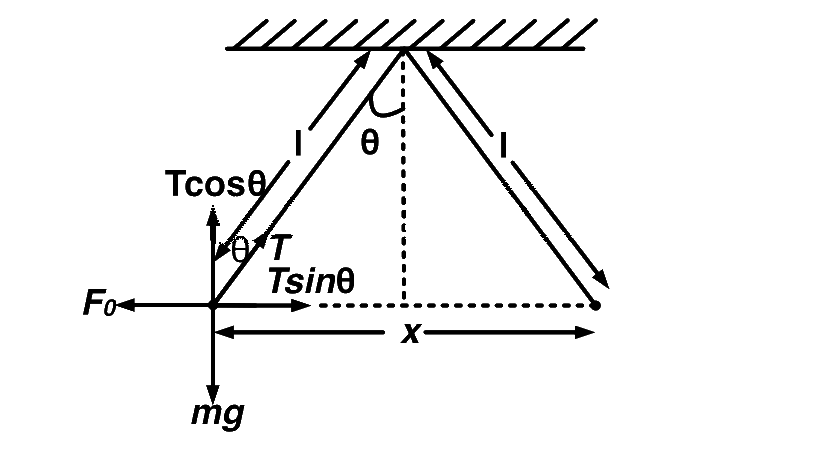
At any instant
$$T\cos \theta = mg\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)$$
$$T\sin \theta = {F_e}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)$$
$$ \Rightarrow {{\sin \theta } \over {\cos \theta }} = {{{F_e}} \over {mg}} \Rightarrow {F_e} = mg\,\tan \theta $$
$$ \Rightarrow {{k{q^2}} \over {{x^2}}} = mg\,\tan \theta \Rightarrow {q^2} \propto {x^2}\tan \theta $$
$$\sin \theta = {\textstyle{x \over {2l}}}$$
For small $$\theta ,\,\sin \theta \approx \tan \theta $$
$$\therefore$$ $${q^2} \propto {x^3}$$
$$ \Rightarrow q{{dq} \over {dt}} \propto {x^2}{{dx} \over {dt}}$$
$$\therefore$$ $${{dq} \over {dt}} = const.$$
$$\therefore$$ $$q \propto {x^2}.v \Rightarrow {x^{3/2}}\alpha {x^2}.v\,\,$$ $$\,\,\,\,\,$$ $$\left[ {\,\,} \right.$$ as $$\left. {{q^2} \propto {x^3}\,\,} \right]$$
$$ \Rightarrow v \propto {x^{ - 1/2}}$$
$$T\cos \theta = mg\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)$$
$$T\sin \theta = {F_e}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)$$
$$ \Rightarrow {{\sin \theta } \over {\cos \theta }} = {{{F_e}} \over {mg}} \Rightarrow {F_e} = mg\,\tan \theta $$
$$ \Rightarrow {{k{q^2}} \over {{x^2}}} = mg\,\tan \theta \Rightarrow {q^2} \propto {x^2}\tan \theta $$
$$\sin \theta = {\textstyle{x \over {2l}}}$$
For small $$\theta ,\,\sin \theta \approx \tan \theta $$
$$\therefore$$ $${q^2} \propto {x^3}$$

$$ \Rightarrow q{{dq} \over {dt}} \propto {x^2}{{dx} \over {dt}}$$
$$\therefore$$ $${{dq} \over {dt}} = const.$$
$$\therefore$$ $$q \propto {x^2}.v \Rightarrow {x^{3/2}}\alpha {x^2}.v\,\,$$ $$\,\,\,\,\,$$ $$\left[ {\,\,} \right.$$ as $$\left. {{q^2} \propto {x^3}\,\,} \right]$$
$$ \Rightarrow v \propto {x^{ - 1/2}}$$
Comments (0)


