JEE MAIN - Physics (2010 - No. 6)
In the circuit shown below, the key $$K$$ is closed at $$t=0.$$ The current through the battery is
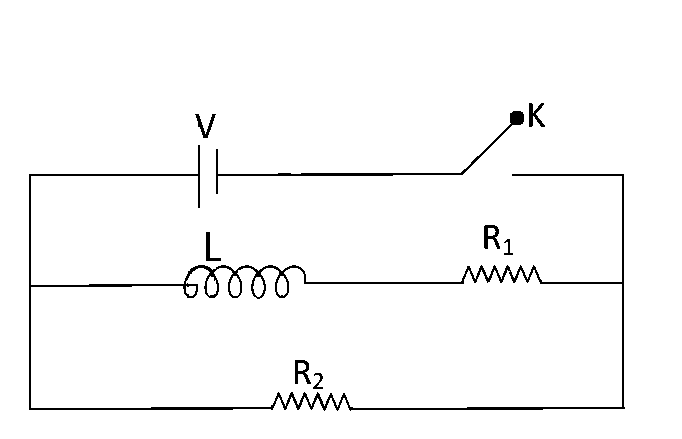

$${{V{R_1}{R_2}} \over {\sqrt {R_1^2 + R_2^2} }}$$ at $$t=0$$ and $${V \over {{R_2}}}$$ at $$t = \infty $$
$${V \over {{R_2}}}$$ at $$\,t = 0$$ and $${{V\left( {{R_1} + {R_2}} \right)} \over {{R_1}{R_2}}}$$ at $$t = \infty $$
$${V \over {{R_2}}}$$ at $$\,t = 0$$ and $${{V{R_1}{R_2}} \over {\sqrt {R_1^2 + R_2^2} }}$$ at $$t = \infty $$
$${{V\left( {{R_1} + {R_2}} \right)} \over {{R_1}{R_2}}}$$ at $$t=0$$ and $${V \over {{R_2}}}$$ at $$t = \infty $$
Explanation
At $$t=0,$$ no current will flow through $$L$$ and $${R_1}$$
$$\therefore$$ Current through battery $$ = {V \over {{R_2}}}$$
At $$t = \infty ,$$
effective resistance, $${{\mathop{\rm R}\nolimits} _{eff}} = {{{R_1}{R_2}} \over {{R_1} + {R_2}}}$$
$$\therefore$$ Current through battery $$ = {V \over {{{\mathop{\rm R}\nolimits} _{eff}}}} = {{V\left( {{R_1} + {R_2}} \right)} \over {{R_1}{R_2}}}$$
$$\therefore$$ Current through battery $$ = {V \over {{R_2}}}$$
At $$t = \infty ,$$
effective resistance, $${{\mathop{\rm R}\nolimits} _{eff}} = {{{R_1}{R_2}} \over {{R_1} + {R_2}}}$$
$$\therefore$$ Current through battery $$ = {V \over {{{\mathop{\rm R}\nolimits} _{eff}}}} = {{V\left( {{R_1} + {R_2}} \right)} \over {{R_1}{R_2}}}$$
Comments (0)


