JEE MAIN - Physics (2010 - No. 26)
For a particle in uniform circular motion the acceleration $$\overrightarrow a $$ at a point P(R, θ) on the circle of radius R is (here θ is measured from the x–axis)
$$ - {{{v^2}} \over R}\cos \theta \widehat i + {{{v^2}} \over R}\sin \theta \widehat j$$
$$ - {{{v^2}} \over R}\sin \theta \widehat i + {{{v^2}} \over R}\cos \theta \widehat j$$
$$ - {{{v^2}} \over R}\cos \theta \widehat i - {{{v^2}} \over R}\sin \theta \widehat j$$
$${{{v^2}} \over R}\widehat i + {{{v^2}} \over R}\widehat j$$
Explanation
For a particle in uniform circular motion,
$${a_c} = {{{v^2}} \over R}$$ towards the center of the circle
From figure, $$\overrightarrow a = {a_c}\cos \theta \left( { - \widehat i} \right) + {a_c}\sin \theta \left( { - \widehat j} \right)$$
$$ = {{ - {v^2}} \over R}\cos \theta \widehat i - {{{v^2}} \over R}\sin \theta \widehat j$$
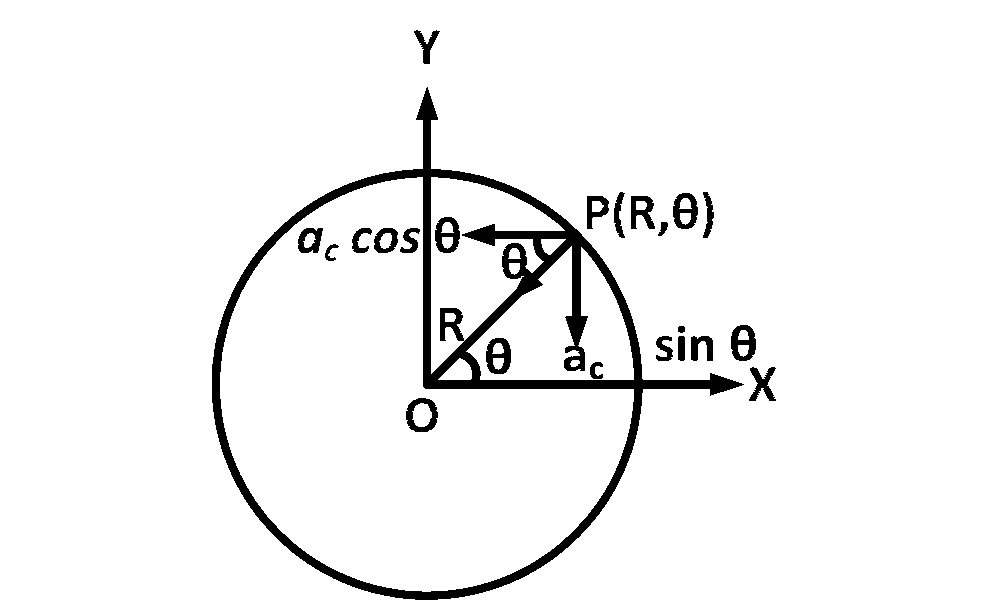
$${a_c} = {{{v^2}} \over R}$$ towards the center of the circle
From figure, $$\overrightarrow a = {a_c}\cos \theta \left( { - \widehat i} \right) + {a_c}\sin \theta \left( { - \widehat j} \right)$$
$$ = {{ - {v^2}} \over R}\cos \theta \widehat i - {{{v^2}} \over R}\sin \theta \widehat j$$

Comments (0)


