JEE MAIN - Physics (2010 - No. 23)
Two identical charged spheres are suspended by strings of equal lengths. The strings make an angle of $${30^ \circ }$$ with each other. When suspended in a liquid of density $$0.8g$$ $$c{m^{ - 3}},$$ the angle remains the same. If density of the material of the sphere is $$1.6$$ $$g$$ $$c{m^{ - 3}},$$ the dielectric constant of the liquid is
$$4$$
$$3$$
$$2$$
$$1$$
Explanation
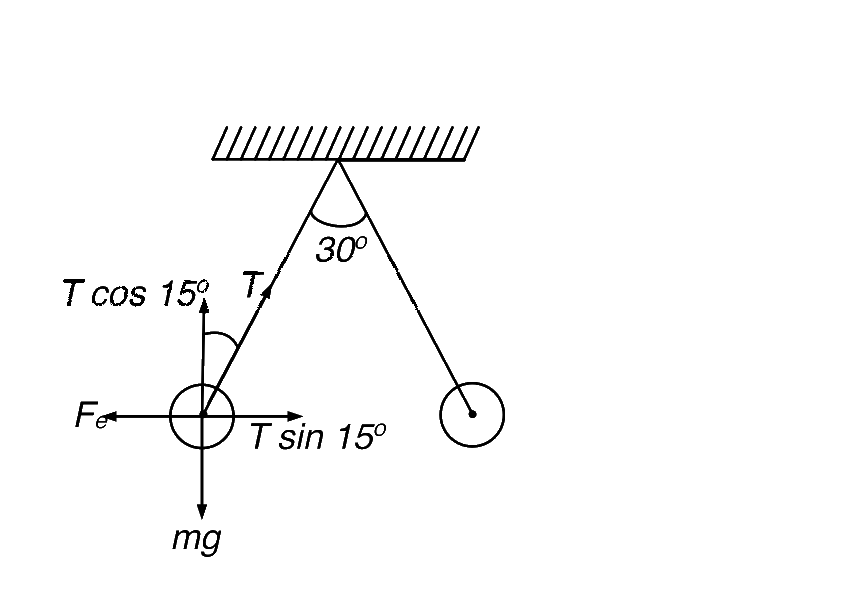
$${F_e} = T\sin {15^ \circ }\,\,;$$
$$mg = T\cos {15^ \circ }$$
$$ \Rightarrow \tan {15^ \circ } = {{{F_e}} \over {mg}}$$ $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...(i)$$
In liquid, $${F_e}' = T'\sin {15^ \circ }$$ $$\,\,\,\,\,\,...(ii)$$
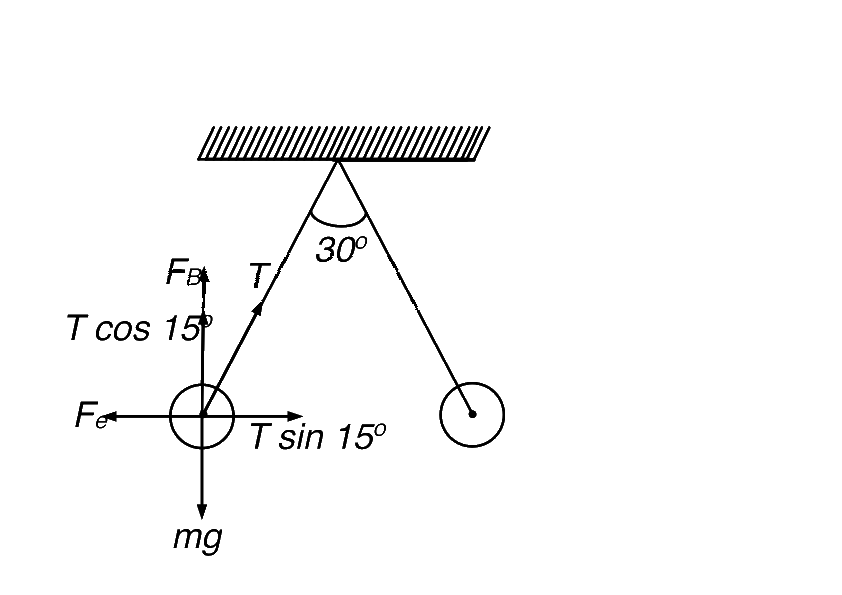
$$mg = {F_B} + T'\cos {15^ \circ }$$
$${F_B}' = V\left( {d - \rho } \right)g = V\left( {1.6 - 0.8} \right)g = 0.8\,Vg$$
$$ = 0.8{m \over d}g = {{0.8mg} \over {1.6}} = {{mg} \over 2}$$
$$\therefore$$ $$mg = {{mg} \over 2} + T'\cos {15^ \circ }$$
$$ \Rightarrow {{mg} \over 2} = T'\cos {15^ \circ }$$ $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( B \right)$$
From $$(A)$$ and $$(B),$$ $$\tan \,{15^ \circ } = {{2{F_e}'} \over {mg}}\,\,\,\,\,\,\,\,\,...\left( 2 \right)$$
From $$(1)$$ and $$(2)$$
$${{{F_e}} \over {mg}} = {{2{F_e}'} \over {mg}} \Rightarrow {F_e} = 2{F_e}' \Rightarrow {F_e}' = {{{F_e}} \over 2}$$
Comments (0)


