JEE MAIN - Physics (2010 - No. 22)
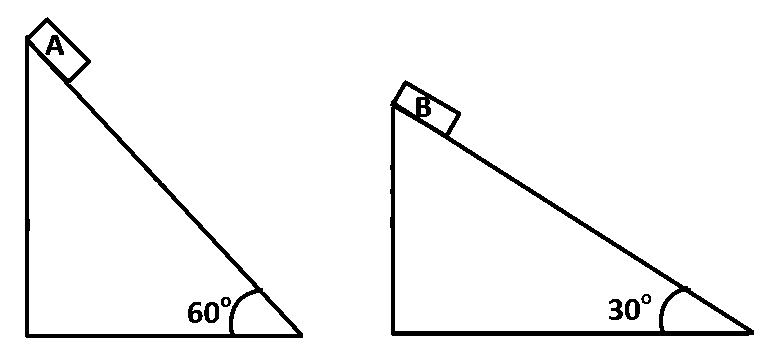
Two fixed frictionless inclined planes making an angle $${30^ \circ }$$ and $${60^ \circ }$$ with the vertical are shown in the figure. Two blocks $$A$$ and $$B$$ are placed on the two planes. What is the relative vertical acceleration of $$A$$ with respect to $$B$$ ?

$$4.9m{s^{ - 2}}$$ in horizontal direction
$$9.8m{s^{ - 2}}$$ in vertical direction
Zero
$$4.9m{s^{ - 2}}$$ in vertical direction
Explanation
Along inclined plane the equation of motion of the body
$$mg\,\sin \,\theta = ma$$ $$\,\,\,\,\,\,\,\,$$ $$\therefore$$ $$a = g\,\sin \,\theta $$
where $$a$$ is along the inclined plane.
$$\therefore$$ vertical component of acceleration is $$\left( {g\sin \theta } \right)\sin \theta $$ = $$g\,{\sin ^2}\theta $$ (Along vertical)
For block A,
$${a_{A\left( {along\,vertical} \right)}} = g{\sin ^2}60^\circ $$
For block B,
$${a_{B\left( {along\,vertical} \right)}} = g{\sin ^2}30^\circ $$
$$\therefore$$ relative vertical acceleration of $$A$$ with respect to $$B$$ is
$$g{\sin ^2}60^\circ $$ - $$g{\sin ^2}30^\circ $$
=$$g\left( {{{\sin }^2}60 - {{\sin }^2}\left. {30} \right]} \right.$$
$$= 4.9$$ $$\,\,m/{s^2}$$ in vertical direction
$$mg\,\sin \,\theta = ma$$ $$\,\,\,\,\,\,\,\,$$ $$\therefore$$ $$a = g\,\sin \,\theta $$
where $$a$$ is along the inclined plane.
$$\therefore$$ vertical component of acceleration is $$\left( {g\sin \theta } \right)\sin \theta $$ = $$g\,{\sin ^2}\theta $$ (Along vertical)
For block A,
$${a_{A\left( {along\,vertical} \right)}} = g{\sin ^2}60^\circ $$
For block B,
$${a_{B\left( {along\,vertical} \right)}} = g{\sin ^2}30^\circ $$
$$\therefore$$ relative vertical acceleration of $$A$$ with respect to $$B$$ is
$$g{\sin ^2}60^\circ $$ - $$g{\sin ^2}30^\circ $$
=$$g\left( {{{\sin }^2}60 - {{\sin }^2}\left. {30} \right]} \right.$$
$$= 4.9$$ $$\,\,m/{s^2}$$ in vertical direction
Comments (0)


