JEE MAIN - Physics (2010 - No. 19)
Let there be a spherically symmetric charge distribution with charge density varying as $$\rho \left( r \right) = {\rho _0}\left( {{5 \over 4} - {r \over R}} \right)$$ upto $$r=R,$$ and $$\rho \left( r \right) = 0$$ for $$r>R,$$ where $$r$$ is the distance from the erigin. The electric field at a distance $$r\left( {r < R} \right)$$ from the origin is given by
$${{{\rho _0}r} \over {4{\varepsilon _0}}}\left( {{5 \over 3} - {r \over R}} \right)$$
$${{4\pi {\rho _0}r} \over {3{\varepsilon _0}}}\left( {{5 \over 3} - {r \over R}} \right)$$
$${{4{\rho _0}r} \over {4{\varepsilon _0}}}\left( {{5 \over 4} - {r \over R}} \right)$$
$${{{\rho _0}r} \over {3{\varepsilon _0}}}\left( {{5 \over 4} - {r \over R}} \right)$$
Explanation
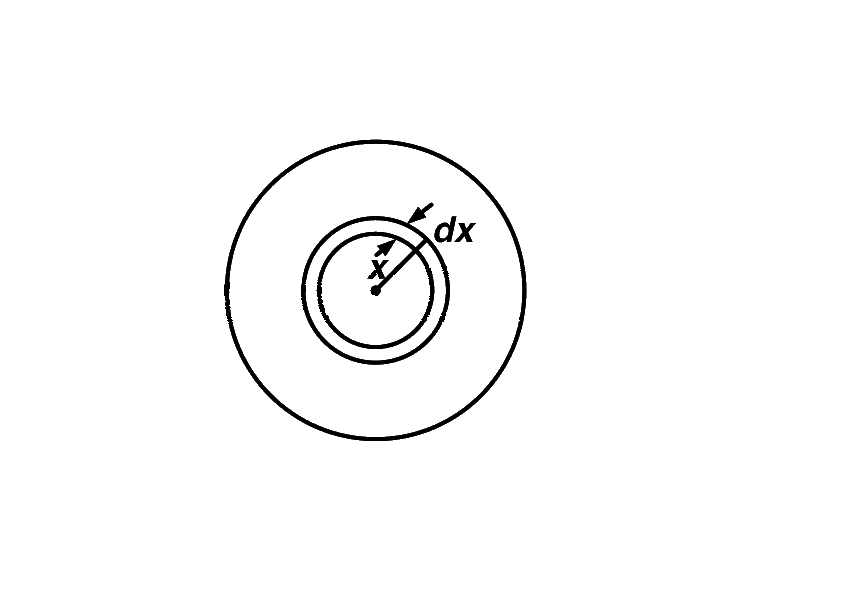
Let us consider a spherical shell of radius $$x$$ and thickness $$dx.$$
Charge on this shell
$$dq = \rho .4{\pi ^2}dx = {\rho _0}\left( {{5 \over 4} - {x \over R}} \right).4\pi {x^2}dx$$
$$\therefore$$ Total charge in the spherical region from center to $$r$$ $$\left( {r < R} \right)$$ is
$$q = \int {dq = 4\pi {\rho _0}\int\limits_0^r {\left( {{5 \over 4} - {x \over R}} \right)} } {x^2}dx$$
$$ = 4\pi {\rho _0}\left[ {{5 \over 4}.{{{r^3}} \over 3} - {1 \over R}.{{{r^4}} \over 4}} \right]$$
$$ = \pi {\rho _0}{r^3}\left( {{5 \over 3} - {r \over R}} \right)$$
$$\therefore$$ Electric field at $$r,$$ $$E = {1 \over {4\pi { \in _0}}}.{q \over {{r^2}}}$$
$$ = {1 \over {4\pi { \in _0}}}.{{\pi {\rho _0}{r^3}} \over {{r^2}}}\left( {{5 \over 3} - {r \over R}} \right)$$
$$ = {{{\rho _0}r} \over {4{ \in _0}}}\left( {{5 \over 3} - {r \over R}} \right)$$
Comments (0)


