JEE MAIN - Physics (2010 - No. 18)
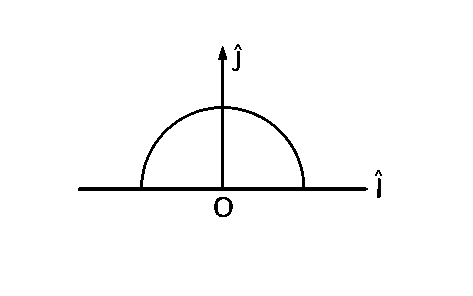
A thin semi-circular ring of radius $$r$$ has a positive charges $$q$$ distributed uniformly over it. The net field $$\overrightarrow E $$ at the center $$O$$ is

$${q \over {4{\pi ^2}{\varepsilon _0}{r^2}}}\,j$$
$$ - {q \over {4{\pi ^2}{\varepsilon _0}{r^2}}}\,j$$
$$ - {q \over {2{\pi ^2}{\varepsilon _0}{r^2}}}\,j$$
$$ {q \over {2{\pi ^2}{\varepsilon _0}{r^2}}}\,j$$
Explanation
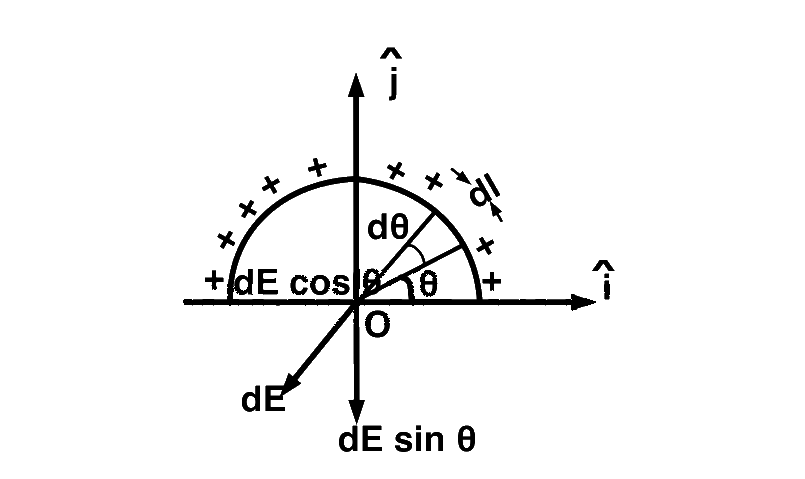
Let us consider a differential element $$dl.$$ charge on this element.
$$dq = \left( {{q \over {\pi r}}} \right)dl$$
$$ = {q \over {\pi r}}\left( {rd\theta } \right)\,\,\,\,\,$$ (as $$dl = rd\theta $$)
$$ = \left( {{q \over \pi }} \right)d\theta $$
Electric field at $$O$$ due to $$dq$$ is
$$dE = {1 \over {4\pi { \in _0}}}.{{dq} \over {{r^2}}}$$
$$ = {1 \over {4\pi { \in _0}}}.{q \over {\pi {r^2}}}d\theta $$
The component $$dE\cos \theta $$ will be counter balanced by another element on left portion.
Hence resultant field at $$O$$ is the resultant of the component $$dE\sin \theta $$ only.
$$\therefore$$ $$E = \int {dE\sin \theta = \int\limits_0^\pi {{q \over {4{\pi ^2}{r^2}{ \in _0}}}} } \sin \theta d\theta $$
$$ = {q \over {4{\pi ^2}{r^2}{ \in _0}}}\left[ { - \cos \theta } \right]_0^\pi $$
$$ = {q \over {4{\pi ^2}{r^2}{ \in _0}}}\left( { + 1 + 1} \right)$$
$$ = {q \over {2{\pi ^2}{r^2}{ \in _0}}}$$
The directions of $$E$$ is towards negative $$y$$-axis.
$$\therefore$$ $$\overrightarrow E = - {q \over {2{\pi ^2}{r^2}{ \in _0}}}\widehat j$$
Comments (0)


