JEE MAIN - Physics (2010 - No. 12)
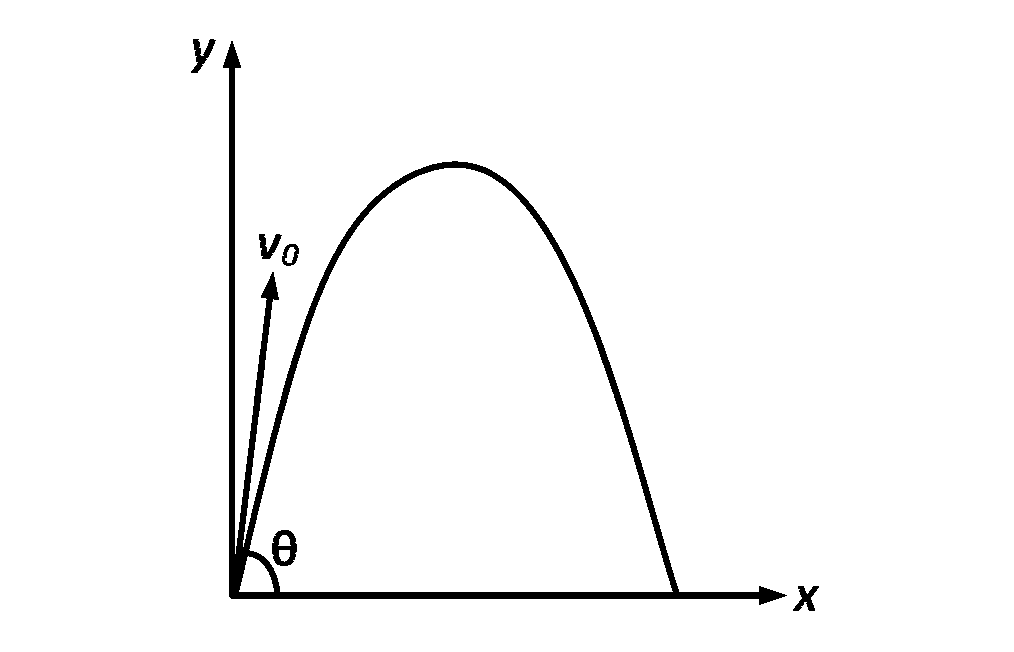
A small particle of mass $$m$$ is projected at an angle $$\theta $$ with the $$x$$-axis with an initial velocity $${v_0}$$ in the $$x$$-$$y$$ plane as shown in the figure. At a time $$t < {{{v_0}\sin \theta } \over g},$$ the angular momentum of the particle is ................,
where $$\widehat i,\widehat j$$ and $$\widehat k$$ are unit vectors along $$x,y$$ and $$z$$-axis respectively.

where $$\widehat i,\widehat j$$ and $$\widehat k$$ are unit vectors along $$x,y$$ and $$z$$-axis respectively.
$$ - mg\,{v_0}{t^2}\cos \theta \widehat j$$
$$mg\,{v_0}t\cos \theta \widehat k$$
$$ - {1 \over 2}mg\,{v_0}{t^2}\cos \,\theta \widehat k$$
$${1 \over 2}mg\,{v_0}{t^2}\cos \theta \widehat i$$
Explanation
Position vector of the particle from the original at any time t is
$$\overrightarrow r = {v_0}t\cos \theta \widehat i + \left( {{v_0}t\sin \theta - {1 \over 2}g{t^2}} \right)\widehat j$$
As Velocity vector, $$\overrightarrow v = {{d\overrightarrow r } \over {dt}}$$
$$\therefore$$ $$\overrightarrow v = {d \over {dt}}\left( {{v_0}t\cos \theta \widehat i + \left( {{v_0}t\sin \theta - {1 \over 2}g{t^2}} \right)\widehat j} \right)$$
$$ = {v_0}\cos \theta \widehat i + \left( {{v_0}\sin \theta - gt} \right)\widehat j$$
Angular momentum of the particle about the origin is
$$\overrightarrow L = m\left( {\overrightarrow r \times \overrightarrow v } \right)$$
$$\eqalign{ & \overrightarrow L = m\left[ {{v_0}\,\cos \theta t\widehat i + \left( {{v_0}\,\sin \theta t - {1 \over 2}g{t^2}} \right)\widehat j} \right] \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left[ {{v_0}\,\cos \,\theta \widehat i + \left( {{v_0}\,\sin \theta - gt} \right)\widehat j} \right] \cr} $$
$$ = m{v_0}\cos \theta t\left[ { - {1 \over 2}gt} \right]\widehat k$$
$$ = - {1 \over 2}mg{v_0}{t^2}\cos \theta \widehat k$$
$$\overrightarrow r = {v_0}t\cos \theta \widehat i + \left( {{v_0}t\sin \theta - {1 \over 2}g{t^2}} \right)\widehat j$$
As Velocity vector, $$\overrightarrow v = {{d\overrightarrow r } \over {dt}}$$
$$\therefore$$ $$\overrightarrow v = {d \over {dt}}\left( {{v_0}t\cos \theta \widehat i + \left( {{v_0}t\sin \theta - {1 \over 2}g{t^2}} \right)\widehat j} \right)$$
$$ = {v_0}\cos \theta \widehat i + \left( {{v_0}\sin \theta - gt} \right)\widehat j$$
Angular momentum of the particle about the origin is
$$\overrightarrow L = m\left( {\overrightarrow r \times \overrightarrow v } \right)$$
$$\eqalign{ & \overrightarrow L = m\left[ {{v_0}\,\cos \theta t\widehat i + \left( {{v_0}\,\sin \theta t - {1 \over 2}g{t^2}} \right)\widehat j} \right] \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left[ {{v_0}\,\cos \,\theta \widehat i + \left( {{v_0}\,\sin \theta - gt} \right)\widehat j} \right] \cr} $$
$$ = m{v_0}\cos \theta t\left[ { - {1 \over 2}gt} \right]\widehat k$$
$$ = - {1 \over 2}mg{v_0}{t^2}\cos \theta \widehat k$$
Comments (0)


