JEE MAIN - Physics (2010 - No. 11)
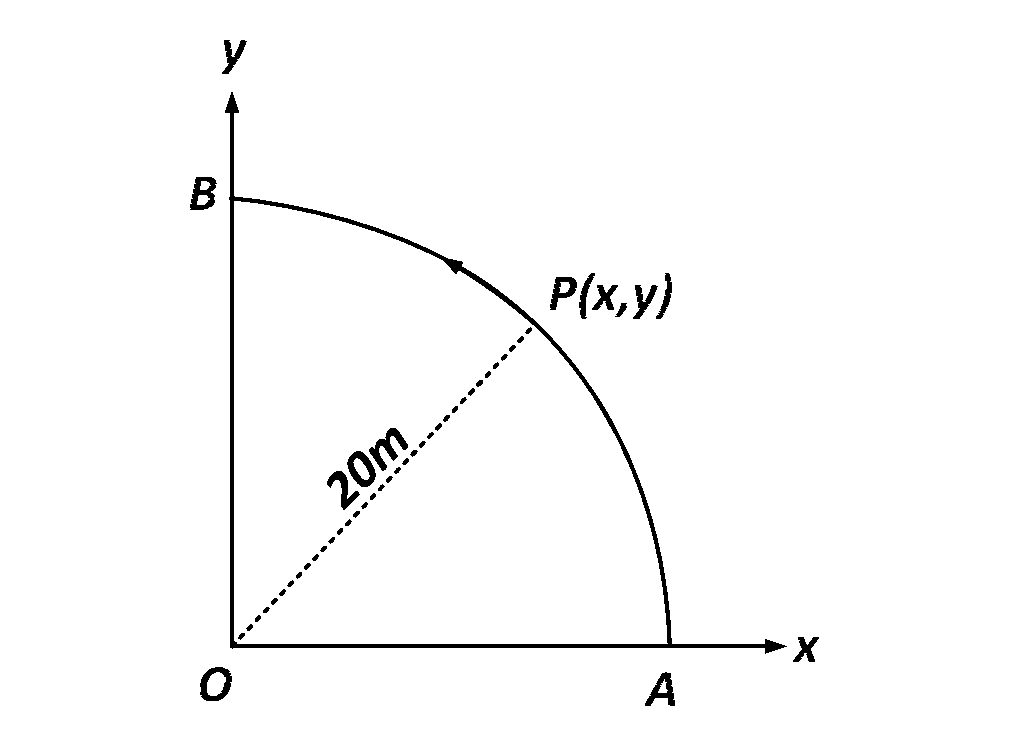
A point $$P$$ moves in counter-clockwise direction on a circular path as shown in the figure. The movement of $$P$$ is such that it sweeps out a length $$s = {t^3} + 5,$$ where $$s$$ is in metres and $$t$$ is in seconds. The radius of the path is $$20$$ $$m.$$ The acceleration of $$'P'$$ when $$t=2$$ $$s$$ is nearly.

$$13m/{s_2}$$
$$12m/{s^2}$$
$$7.2m{s^2}$$
$$14m/{s^2}$$
Explanation
Given $$s = {t^3} + 5 $$
$$\Rightarrow$$ Speed,$$\,\,\,v = {{ds} \over {dt}} = 3{t^2}$$
Tangential acceleration $${a_t} = {{dv} \over {dt}} = 6t$$
Radial acceleration $${a_c} = {{{v^2}} \over R} = {{9{t^4}} \over R}$$
At $$\,\,\,\,t = 2s,\,\,{a_t} = 6 \times 2 = 12\,\,m/{s^2}$$
$${a_c} = {{9 \times 16} \over {20}} = 7.2\,\,m/{s^2}$$
$$\therefore$$ Net acceleration
$$ = \sqrt {a_t^2 + a_c^2} $$
$$= \sqrt {{{\left( {12} \right)}^2} + {{\left( {7.2} \right)}^2}} $$
$$ = \sqrt {144 + 51.84} $$
$$ = \sqrt {195.84} $$
$$ = 14\,m/{s^2}$$
$$\Rightarrow$$ Speed,$$\,\,\,v = {{ds} \over {dt}} = 3{t^2}$$
Tangential acceleration $${a_t} = {{dv} \over {dt}} = 6t$$
Radial acceleration $${a_c} = {{{v^2}} \over R} = {{9{t^4}} \over R}$$
At $$\,\,\,\,t = 2s,\,\,{a_t} = 6 \times 2 = 12\,\,m/{s^2}$$
$${a_c} = {{9 \times 16} \over {20}} = 7.2\,\,m/{s^2}$$
$$\therefore$$ Net acceleration
$$ = \sqrt {a_t^2 + a_c^2} $$
$$= \sqrt {{{\left( {12} \right)}^2} + {{\left( {7.2} \right)}^2}} $$
$$ = \sqrt {144 + 51.84} $$
$$ = \sqrt {195.84} $$
$$ = 14\,m/{s^2}$$
Comments (0)


