JEE MAIN - Physics (2008 - No. 25)
A spherical solid ball of volume $$V$$ is made of a material of density $${\rho _1}$$. It is falling through a liquid of density $${\rho _2}\left( {{\rho _2} < {\rho _1}} \right)$$. Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed $$v,$$ i.e., $${F_{viscous}} = - k{v^2}\left( {k > 0} \right).$$ The terminal speed of the ball is
$$\sqrt {{{Vg\left( {{\rho _1} - {\rho _2}} \right)} \over k}} $$
$${{{Vg{\rho _1}} \over k}}$$
$$\sqrt {{{Vg{\rho _1}} \over k}} $$
$${{Vg\left( {{\rho _1} - {\rho _2}} \right)} \over k}$$
Explanation
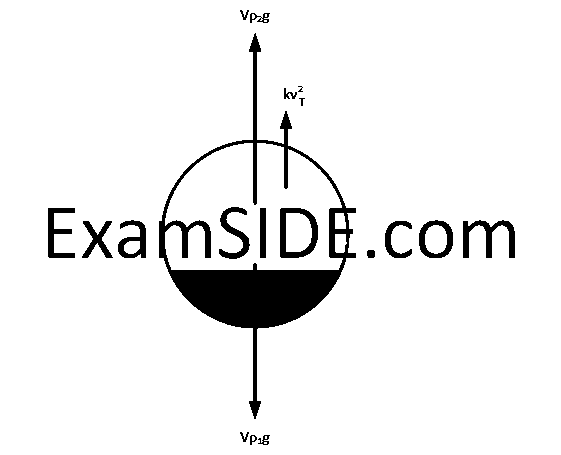
The forces acting on the ball -
(1) mg = $$V{\rho _1}g$$ downward direction
(2) Thrust upward direction ( By Archimedes principle )
(3) Force of friction ( Buoynat force) upward direction
The ball reaches to its terminal speed $$\left( {{v_t}} \right)$$ when acceleration = 0.
So, weight $$=$$ Buoyant force $$+$$ Viscous force
$$\therefore$$ $$V\rho {}_1g = V{\rho _2}g + kv_t^2$$
$$\therefore$$ $${v_t} = \sqrt {{{Vg\left( {{\rho _1} - {\rho _2}} \right)} \over k}} $$
Comments (0)


