JEE MAIN - Physics (2008 - No. 22)
A thin rod of length $$'L'$$ is lying along the $$x$$-axis with its ends at $$x=0$$ and $$x=L$$. Its linear density (mass/length) varies with $$x$$ as $$k{\left( {{x \over L}} \right)^n},$$ where $$n$$ can be zero or any positive number. If the position $${X_{CM}}$$ of the center of mass of the rod is plotted against $$'n',$$ which of the following graphs best approximates the dependence of $${X_{CM}}$$ on $$n$$?
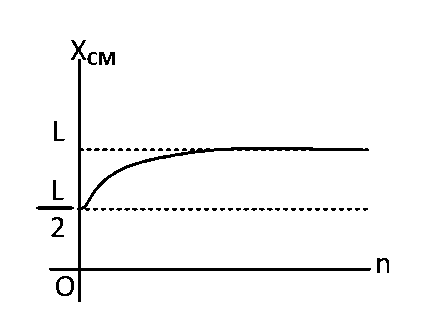
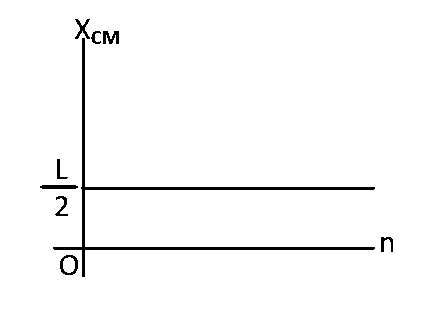
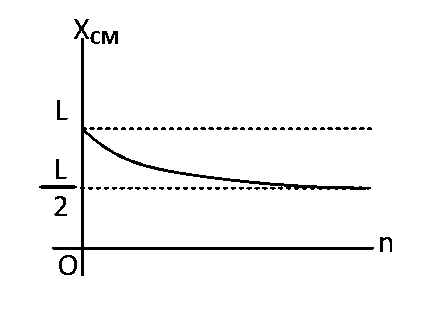
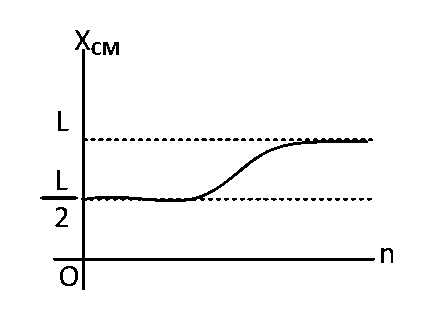
Explanation
Given The linear mass density $$\lambda = k{\left( {{x \over L}} \right)^n}$$
$${x_{CM}} = {{\int\limits_0^L {x{\mkern 1mu} dm} } \over {\int\limits_0^L {dm} }}$$
$$ = {{\int\limits_0^L {x\left( {\lambda {\mkern 1mu} dx} \right)} } \over {\int\limits_0^L {\lambda {\mkern 1mu} dx} }}$$
$$ = {{\int\limits_0^L {k{{\left( {{x \over L}} \right)}^n}} .xdx} \over {\int\limits_0^L {k{{\left( {{x \over L}} \right)}^n}{\mkern 1mu} dx} }}$$
= $${{k\left[ {{{{x^{n + 2}}} \over {\left( {n + 2} \right){L^n}}}} \right]_0^L} \over {\left[ {{{k{\mkern 1mu} {x^{n + 1}}} \over {\left( {n + 1} \right){L^n}}}} \right]_0^L}}$$
$$ = {{L\left( {n + 1} \right)} \over {n + 2}}$$
For $$n=0,$$ $${x_{CM}} = {L \over 2};n = 1,$$
$${x_{CM}} = {{2L} \over 3};n = 2,\,{x_{CM}} = {{3L} \over 4};\,...$$
From here you can see only option (A) can be the right answer.
Comments (0)


