JEE MAIN - Physics (2008 - No. 17)
A parallel plate capacitor with air between the plates has capacitance of $$9$$ $$pF.$$ The separation between its plates is $$'d'.$$ The space between the plates has dielectric constant $${k_1}$$ $$=3$$ and thickness $${d \over 3}$$ while the other one has dielectric constant $${k_2} = 6$$ and thickness $${{2d} \over 3}$$. Capacitance of the capacitor is now
$$1.8$$ $$pF$$
$$45$$ $$pF$$
$$40.5$$ $$pF$$
$$20.25$$ $$pF$$
Explanation
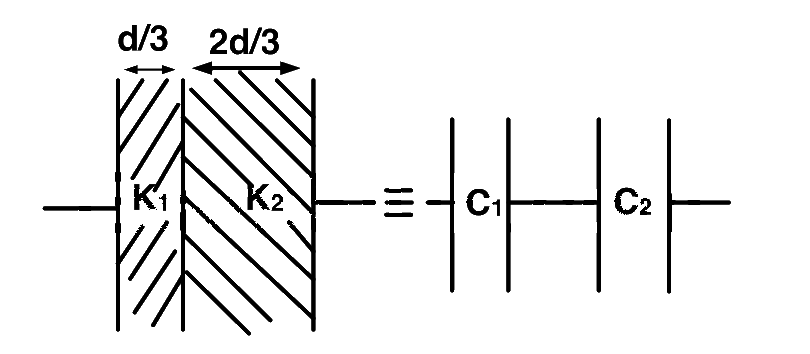
The given capacitance is equal to two capacitances connected in series where
$${C_1} = {{{k_1}{ \in _0}A} \over {d/3}} = {{3{k_1}{ \in _0}A} \over d}$$
$$ = {{3 \times 3{ \in _0}A} \over d} = {{9{ \in _0}A} \over d}$$
and
$${C_2} = {{{k_2}{ \in _0}A} \over {2d/3}} = {{3{k_2}{ \in _0}A} \over {2d}}$$
$$ = {{3 \times 6{ \in _0}A} \over {2d}} = {{9{ \in _0}A} \over d}$$
The equivalent capacitance $${C_{eq}}$$ is
$${1 \over {C{}_{eq}}} = {1 \over {{C_1}}} + {1 \over {{C_2}}}$$
$$ = {d \over {9{ \in _0}A}} + {d \over {9{ \in _0}A}}$$
$$ = {{2d} \over {9{ \in _0}A}}$$
$$\therefore$$ $${C_{eq}} = {9 \over 2}{{{\varepsilon _0}A} \over d} = {9 \over 2} \times 9pF = 40.5pF$$
Comments (0)


