Consider a block of conducting material of resistivity $$'\rho '$$ shown in the figure. Current $$'I'$$ enters at $$'A'$$ and leaves from $$'D'$$. We apply superposition principle to find voltage $$'\Delta V'$$ developed between $$'B'$$ and $$'C'$$. The calculation is done in the following steps:
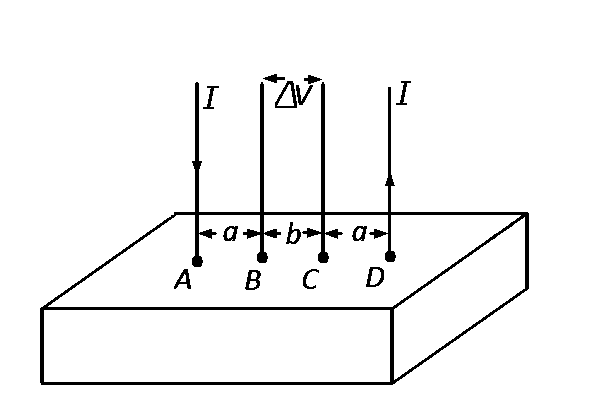
(i) Take current $$'I'$$ entering from $$'A'$$ and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field $$E(r)$$ at distance $$'r'$$ from A by using Ohm's law $$E = \rho j,$$ where $$j$$ is the current per unit area at $$'r'$$.
(iii) From the $$'r'$$ dependence of $$E(r)$$, obtain the potential $$V(r)$$ at $$r$$.
(iv) Repeat (i), (ii) and (iii) for current $$'I'$$ leaving $$'D'$$ and superpose results for $$'A'$$ and $$'D'.$$

For current entering at $$A,$$ the electric field at a distance $$'r'$$ from $$A$$ is