JEE MAIN - Physics (2008 - No. 10)
A $$5V$$ battery with internal resistance $$2\Omega $$ and a $$2V$$ battery with internal resistance $$1\Omega $$ are connected to a $$10\Omega $$ resistor as shown in the figure.
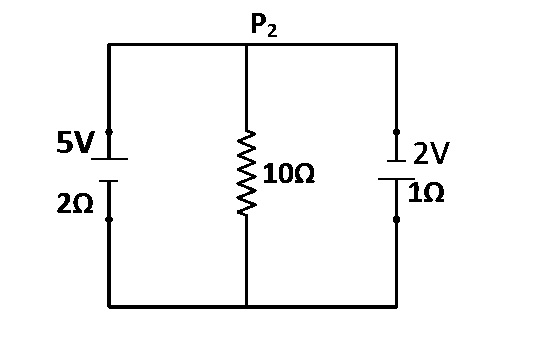

The current in the $$10\Omega $$ resistor is
$$0.27A{P_2}\,\,to\,\,{P_1}$$
$$0.03A{P_1}\,\,to\,\,{P_2}$$
$$0.03A{P_2}\,\,to\,\,{P_1}$$
$$0.27A{P_1}\,\,to\,\,{P_2}$$
Explanation
Applying kirchoff's loop law in $$AB\,{P_2}{P_1}A$$ we get
$$ - 2i + 5 - 10\,{i_1} = 0\,\,\,\,\,\,\,\,...\left( i \right)$$
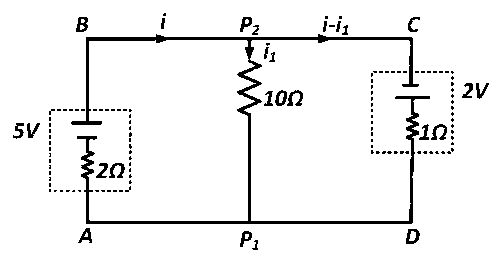
Again applying kirchoffs loop law in $${P_2}$$ $$CD{P_1}{P_2}$$ we get,
$$10{i_1} + 2 - i + {i_1} = 0\,\,\,\,\,\,...\left( {ii} \right)$$
From $$\left( i \right)$$ and $$\left( {ii} \right)$$ $$11{i_1} + 2 - \left[ {{{5 - 10{i_1}} \over 2}} \right] = 0$$
$$ \Rightarrow {i_1} = {1 \over {32}}$$ A from $${P_2}$$ to $${P_1}$$
$$ - 2i + 5 - 10\,{i_1} = 0\,\,\,\,\,\,\,\,...\left( i \right)$$

Again applying kirchoffs loop law in $${P_2}$$ $$CD{P_1}{P_2}$$ we get,
$$10{i_1} + 2 - i + {i_1} = 0\,\,\,\,\,\,...\left( {ii} \right)$$
From $$\left( i \right)$$ and $$\left( {ii} \right)$$ $$11{i_1} + 2 - \left[ {{{5 - 10{i_1}} \over 2}} \right] = 0$$
$$ \Rightarrow {i_1} = {1 \over {32}}$$ A from $${P_2}$$ to $${P_1}$$
Comments (0)


