JEE MAIN - Physics (2007 - No. 35)
A block of mass $$m$$ is connected to another block of $$mass$$ $$M$$ by a spring (massless) of spring constant $$k.$$ The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force $$F$$ starts acting on the block of mass $$M$$ to pull it. Find the force of the block of mass $$m.$$
$${{MF} \over {\left( {m + M} \right)}}$$
$${{mF} \over M}$$
$${{\left( {M + m} \right)F} \over m}$$
$${{mF} \over {\left( {m + M} \right)}}$$
Explanation
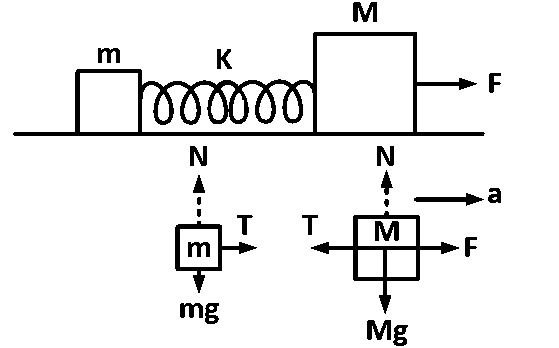
From free body-diagram of $$m$$
we get $$T = ma$$
From free body-diagram of $$M$$
we get $$F-T=Ma$$
where $$T$$ is force due to spring
$$ \Rightarrow F - ma = Ma$$
$$ \Rightarrow$$ $$F=Ma+ma$$
$$\therefore$$ $$a = {F \over {M + m}}$$
Now, force acting on the block of mass $$m$$ is
$$ma = m\left( {{F \over {M + m}}} \right) = {{mF} \over {m + M}}.$$
Comments (0)


