JEE MAIN - Physics (2007 - No. 34)
A circular disc of radius $$R$$ is removed from a bigger circular disc of radius $$2R$$ such that the circumferences of the discs coincide. The center of mass of the new disc is $$\alpha R$$ form the center of the bigger disc. The value of $$\alpha $$ is
$$1/4$$
$$1/3$$
$$1/2$$
$$1/6$$
Explanation
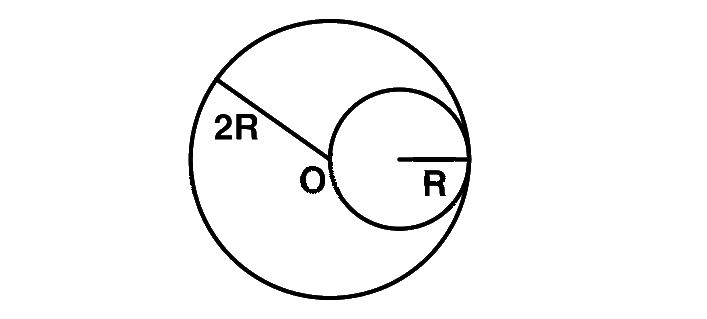
Let the mass per unit area be $$\sigma .$$
Then the mass of the complete disc
$$ = \sigma \left[ {\pi {{\left( {2R} \right)}^2}} \right] = 4\pi \sigma {R^2}$$
The mass of the removed disc $$ = \sigma \left( {\pi {R^2}} \right) = \pi \sigma {R^2}$$
So mass of the remaining disc = $$4\pi \sigma {R^2}$$ - $$\pi \sigma {R^2}$$ = $$3\pi \sigma {R^2}$$
Let center of mass of $$3\pi \sigma {R^2}$$ mass is at x distance from origin O.
$$\therefore$$ $${{3\pi {R^2}\sigma .x + \pi {R^2}\sigma .R} \over {4\pi {R^2}\sigma }} = 0$$
As center of mass of full disc is at Origin.
$$\therefore$$ $$x = - {R \over 3}$$
According to the question, $$x$$ = $$\alpha R$$
$$\therefore$$ $$\alpha = - {1 \over 3}$$
$$ \Rightarrow $$ $$\left| \alpha \right| = {1 \over 3}$$
Comments (0)


