JEE MAIN - Physics (2007 - No. 30)
For the given uniform square lamina $$ABCD$$, whose center is $$O,$$
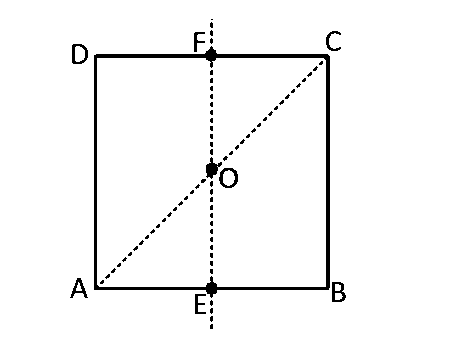

$${I_{AC}} = \sqrt 2 \,\,{I_{EF}}$$
$$\sqrt 2 {I_{AC}} = {I_{EF}}$$
$${I_{AD}} = 3{I_{EF}}$$
$${I_{AC}} = {I_{EF}}$$
Explanation
By perpendicular axes theorem,
$${I_x} = {I_x} + {I_y}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$or,\,\,\,\,\,\,\,\,\,\,\,\,\,{I_z} = 2{I_y}$$
( as $${I_x} = {I_y}$$ by symmetry of the figure)
$$\therefore$$ $${I_{EF}} = {{{I_z}} \over 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,....\left( i \right)$$
By perpendicular axes theorem,
$${I_z} = {I_{AC}} + {I_{BD}} = 2{I_{AC}}$$
(As $${I_{AC}} = {I_{BD}}$$ by symmetry of the figure)
$$\therefore$$ $${I_{AC}} = {{{I_z}} \over 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)$$
From $$(i)$$ and $$(ii),$$ we get $${I_{EF}} = {I_{AC}}.$$
Comments (0)


