JEE MAIN - Physics (2007 - No. 28)
One end of a thermally insulated rod is kept at a temperature $${T_1}$$ and the other at $${T_2}$$. The rod is composed of two sections of length $${L_1}$$ and $${L_2}$$ and thermal conductivities $${K_1}$$ and $${K_2}$$ respectively. The temperature at the interface of the two section is
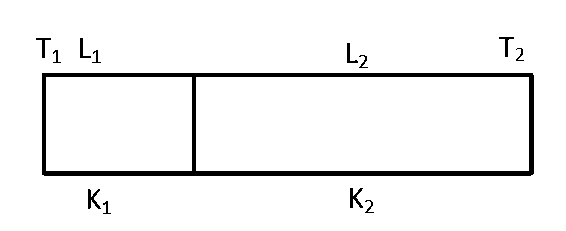

$${{\left( {{K_1}{L_1}{T_1} + {K_2}{L_2}{T_2}} \right)} \over {\left( {{K_1}{L_1} + {K_2}{L_2}} \right)}}$$
$${{\left( {{K_2}{L_2}{T_1} + {K_1}{L_1}{T_2}} \right)} \over {\left( {{K_1}{L_1} + {K_2}{L_2}} \right)}}$$
$${{\left( {{K_2}{L_1}{T_1} + {K_1}{L_2}{T_2}} \right)} \over {\left( {{K_2}{L_1} + {K_1}{L_2}} \right)}}$$
$${{\left( {{K_1}{L_2}{T_1} + {K_2}{L_1}{T_2}} \right)} \over {\left( {{K_1}{L_2} + {K_2}{L_1}} \right)}}$$
Explanation

$${{{K_1}A\left( {{T_1} - T} \right)} \over {{\ell _1}}} = {{{K_2}A\left( {T - {T_2}} \right)} \over {{\ell _2}}}$$
$$\therefore$$ $$T = {{{K_1}{T_1}{\ell _2} + {K_2}{T_2}{\ell _1}} \over {{K_2}{\ell _1} + {K_1}{\ell _2}}}$$
$$ = {{{K_1}{\ell _2}{T_1} + {K_2}{\ell _1}{T_2}} \over {{K_1}{\ell _2} + {K_2}{\ell _1}}}$$
Comments (0)


