JEE MAIN - Physics (2007 - No. 27)
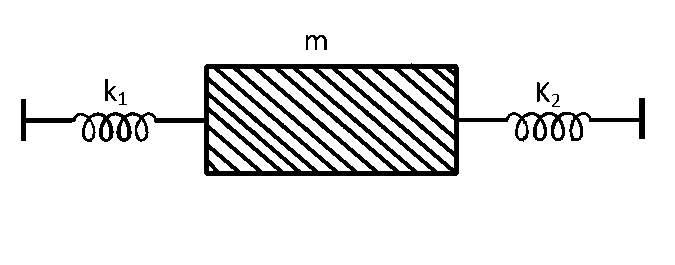
Two springs, of force constant $${k_1}$$ and $${k_2}$$ are connected to a mass $$m$$ as shown. The frequency of oscillation of the mass is $$f.$$ If both $${k_1}$$ and $${k_2}$$ are made four times their original values, the frequency of oscillation becomes

$$2f$$
$$f/2$$
$$f/4$$
$$4f$$
Explanation
The two springs are in parallel.
$$f = {1 \over {2\pi }}\sqrt {{{{K_1} + {K_2}} \over m}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)$$
$$f' = {1 \over {2\pi }}\sqrt {{{4{K_1} + 4{K_2}} \over m}} $$
$$ = {1 \over {2\pi }}\sqrt {{{4\left( {{K_1} + 4{K_2}} \right)} \over m}} $$
$$ = 2\left( {{1 \over {2\pi }}\sqrt {{{{K_1} + {K_2}} \over m}} } \right)$$
$$ = 2f\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ from eqn. $$\left( i \right)$$
$$f = {1 \over {2\pi }}\sqrt {{{{K_1} + {K_2}} \over m}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)$$
$$f' = {1 \over {2\pi }}\sqrt {{{4{K_1} + 4{K_2}} \over m}} $$
$$ = {1 \over {2\pi }}\sqrt {{{4\left( {{K_1} + 4{K_2}} \right)} \over m}} $$
$$ = 2\left( {{1 \over {2\pi }}\sqrt {{{{K_1} + {K_2}} \over m}} } \right)$$
$$ = 2f\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ from eqn. $$\left( i \right)$$
Comments (0)


