JEE MAIN - Physics (2007 - No. 11)
A long straight wire of radius $$a$$ carries a steady current $$i.$$ The current is uniformly distributed across its cross section. The ratio of the magnetic field at $$a/2$$ and $$2a$$ is
$$1/2$$
$$1/4$$
$$4$$
$$1$$
Explanation
Here, current is uniformly distributed across the cross-section of the wire, therefore, current enclosed in the ampere-an path formed at a distance $${r_1}\left( { = {a \over 2}} \right)$$
$$ = \left( {{{\pi r_1^2} \over {\pi {a^2}}}} \right) \times I,$$ where $$I$$ is total current
$$\therefore$$ Magnetic field at $${P_1}$$ is
$${B_1} = {{{\mu _0} \times current\,\,enclosed} \over {path}}$$
$$ \Rightarrow {B_1} = {{{\mu _0} \times \left( {{{\pi r_1^2} \over {\pi {a^2}}}} \right) \times I} \over {2\pi {r_1}}}$$
$$ = {{{\mu _0} \times I{r_1}} \over {2\pi {a^2}}}$$
Now, magnetic field at point $${P_2},$$
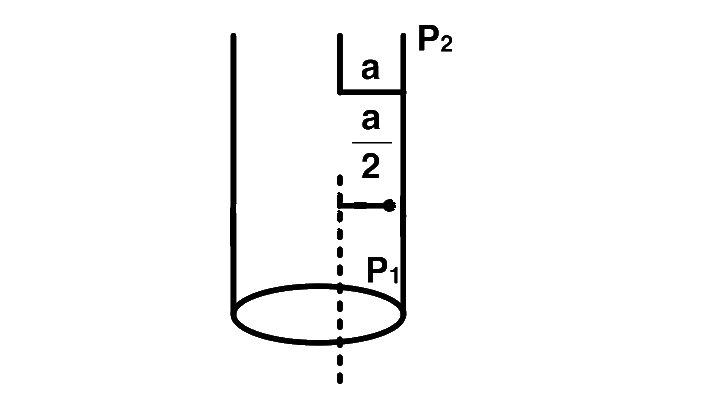
$${B_2} = {{{\mu _0}} \over {2\pi }}.{I \over {\left( {2a} \right)}} = {{{\mu _0}I} \over {4\pi a}}$$
$$\therefore$$ Required ratio $$ = {{{B_1}} \over {{B_2}}} = {{{\mu _0}I{r_1}} \over {2\pi {a^2}}} \times {{4\pi a} \over {{\mu _0}I}}$$
$$ = {{2{r_1}} \over a} = {{2 \times {a \over 2}} \over a} = 1.$$
$$ = \left( {{{\pi r_1^2} \over {\pi {a^2}}}} \right) \times I,$$ where $$I$$ is total current
$$\therefore$$ Magnetic field at $${P_1}$$ is
$${B_1} = {{{\mu _0} \times current\,\,enclosed} \over {path}}$$
$$ \Rightarrow {B_1} = {{{\mu _0} \times \left( {{{\pi r_1^2} \over {\pi {a^2}}}} \right) \times I} \over {2\pi {r_1}}}$$
$$ = {{{\mu _0} \times I{r_1}} \over {2\pi {a^2}}}$$
Now, magnetic field at point $${P_2},$$

$${B_2} = {{{\mu _0}} \over {2\pi }}.{I \over {\left( {2a} \right)}} = {{{\mu _0}I} \over {4\pi a}}$$
$$\therefore$$ Required ratio $$ = {{{B_1}} \over {{B_2}}} = {{{\mu _0}I{r_1}} \over {2\pi {a^2}}} \times {{4\pi a} \over {{\mu _0}I}}$$
$$ = {{2{r_1}} \over a} = {{2 \times {a \over 2}} \over a} = 1.$$
Comments (0)


