JEE MAIN - Physics (2007 - No. 10)
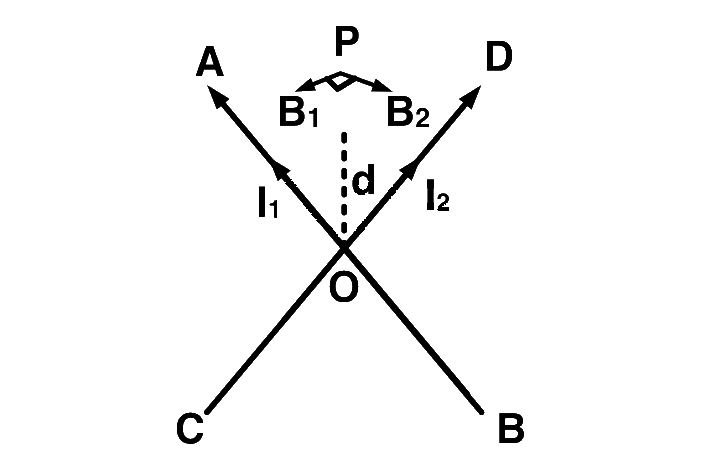
Two identical conducting wires $$AOB$$ and $$COD$$ are placed at right angles to each other. The wire $$AOB$$ carries an electric current $${I_1}$$ and $$COD$$ carries a current $${I_2}$$. The magnetic field on a point lying at a distance $$d$$ from $$O$$, in a direction perpendicular to the plane of the wires $$AOB$$ and $$COD$$ , will be given by
$${{{\mu _0}} \over {2\pi d}}\left( {I_1^2 + I_2^2} \right)$$
$${{{\mu _0}} \over {2\pi }}{\left( {{{{I_1} + {I_2}} \over d}} \right)^{{1 \over 2}}}$$
$${{{\mu _0}} \over {2\pi d}}{\left( {I_1^2 + I_2^2} \right)^{{1 \over 2}}}$$
$${{{\mu _0}} \over {2\pi d}}\left( {{I_1} + {I_2}} \right)$$
Explanation
Clearly, the magnetic fields at a point $$P,$$ equidistant from $$AOB$$ and $$COD$$ will have directions perpendicular to each other, as they are placed normal to each other.
$$\therefore$$ Resultant field, $$B = \sqrt {B_1^2 + B_2^2} $$
But $${B_1} = {{{\mu _0}{I_1}} \over {2\pi d}}$$ and $${B_2} = {{{\mu _0}{I_2}} \over {2\pi d}}$$
$$\therefore$$ $$B = \sqrt {{{\left( {{{{\mu _0}} \over {2\pi d}}} \right)}^2}\left( {I_1^2 + I_2^2} \right)} $$
or, $$B = {{{\mu _0}} \over {2\pi d}}{\left( {I_1^2 + I_2^2} \right)^{1/2}}$$
$$\therefore$$ Resultant field, $$B = \sqrt {B_1^2 + B_2^2} $$
But $${B_1} = {{{\mu _0}{I_1}} \over {2\pi d}}$$ and $${B_2} = {{{\mu _0}{I_2}} \over {2\pi d}}$$
$$\therefore$$ $$B = \sqrt {{{\left( {{{{\mu _0}} \over {2\pi d}}} \right)}^2}\left( {I_1^2 + I_2^2} \right)} $$
or, $$B = {{{\mu _0}} \over {2\pi d}}{\left( {I_1^2 + I_2^2} \right)^{1/2}}$$

Comments (0)


