JEE MAIN - Physics (2006 - No. 6)
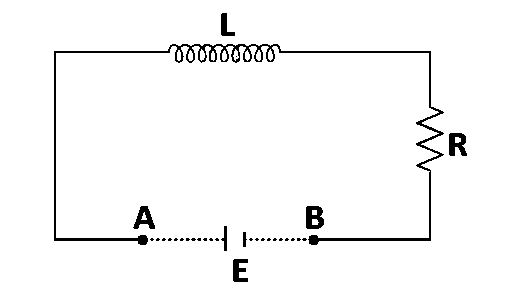
An inductor $$(L=100$$ $$mH)$$, a resistor $$\left( {R = 100\,\Omega } \right)$$ and a battery $$\left( {E = 100V} \right)$$ are initially connected in series as shown in the figure. After a long time the battery is disconnected after short circuiting the points $$A$$ and $$B$$. The current in the circuit $$1$$ $$ms$$ after the short circuit is

$$1/eA$$
$$eA$$
$$0.1$$ $$A$$
$$1$$ $$A$$
Explanation
Initially, when steady state is achieved,
$$i = {E \over R}$$
Let $$E$$ is short circuited at a $$t=0.$$ Then
At $$t=0,$$ $${i_0} = {E \over R}$$
Let during decay of current at any time the current
flowing is $$ - L{{di} \over {dt}} - iR = 0$$
$$ \Rightarrow {{di} \over i} = - {R \over L}dt$$
$$ \Rightarrow \int\limits_{{i_0}}^i {{{di} \over i}} = \int\limits_0^t { - {R \over L}dt} $$
$$ \Rightarrow {\log _e}{i \over {{i_0}}} = - {R \over L}t$$
$$ \Rightarrow i = {i_0}\,{e^{ - {R \over L}t}}$$
$$ \Rightarrow i = {E \over R}{e^{{R \over L}t}} = {{100} \over {100}}{e^{{{ - 100 \times {{10}^{ - 3}}} \over {100 \times {{10}^{ - 3}}}}}} = {1 \over e}$$
$$i = {E \over R}$$
Let $$E$$ is short circuited at a $$t=0.$$ Then
At $$t=0,$$ $${i_0} = {E \over R}$$
Let during decay of current at any time the current
flowing is $$ - L{{di} \over {dt}} - iR = 0$$
$$ \Rightarrow {{di} \over i} = - {R \over L}dt$$
$$ \Rightarrow \int\limits_{{i_0}}^i {{{di} \over i}} = \int\limits_0^t { - {R \over L}dt} $$
$$ \Rightarrow {\log _e}{i \over {{i_0}}} = - {R \over L}t$$
$$ \Rightarrow i = {i_0}\,{e^{ - {R \over L}t}}$$
$$ \Rightarrow i = {E \over R}{e^{{R \over L}t}} = {{100} \over {100}}{e^{{{ - 100 \times {{10}^{ - 3}}} \over {100 \times {{10}^{ - 3}}}}}} = {1 \over e}$$
Comments (0)


