JEE MAIN - Physics (2006 - No. 48)
Consider a two particle system with particles having masses $${m_1}$$ and $${m_2}$$. If the first particle is pushed towards the center of mass through a distance $$d,$$ by what distance should the second particle is moved, so as to keep the center of mass at the same position?
$${{{m_2}} \over {{m_1}}}\,\,d$$
$${{{m_1}} \over {{m_1} + {m_2}}}d$$
$${{{m_1}} \over {{m_2}}}d$$
$$d$$
Explanation
Initially,
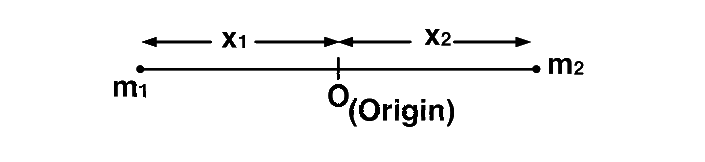
$$0 = {{{m_1}\left( { - {x_1}} \right) + {m_2}{x_2}} \over {{m_1} + {m_2}}} \Rightarrow {m_1}{x_1} = {m_2}{x_2}$$

$$0 = {{{m_1}\left( { - {x_1}} \right) + {m_2}{x_2}} \over {{m_1} + {m_2}}} \Rightarrow {m_1}{x_1} = {m_2}{x_2}$$
Finally,
mass m1 moved towards the center a distance d so the distance of mass m1 from the origin is x1 - d, and now let mass m2 need to move d' to keep the center at the origin.
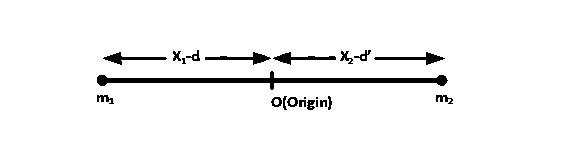
$$\therefore$$ $$0 = {{{m_1}\left( {d - {x_1}} \right) + {m_2}\left( {{x_2} - d'} \right)} \over {{m_1} + {m_2}}}$$
$$ \Rightarrow 0 = {m_1}d - {m_1}{x_1} + {m_2}{x_2} - {m_2}d'$$
$$ \Rightarrow d' = {{{m_1}} \over {{m_2}}}d$$
Comments (0)


