JEE MAIN - Physics (2006 - No. 47)
A bomb of mass $$16kg$$ at rest explodes into two pieces of masses $$4$$ $$kg$$ and $$12$$ $$kg.$$ The velocity of the $$12$$ $$kg$$ mass is $$4\,\,m{s^{ - 1}}.$$ The kinetic energy of the other mass is
$$144$$ $$J$$
$$288$$ $$J$$
$$192$$ $$J$$
$$96$$ $$J$$
Explanation
Here linear momentum is conserved as no external force is acting on the bomb.
Let the velocity and mass of $$4$$ $$kg$$ piece be $${v_1}$$ and $${m_1}$$ and that of $$12$$ $$kg$$ piece be $${v_2}$$ and $${m_2}$$.
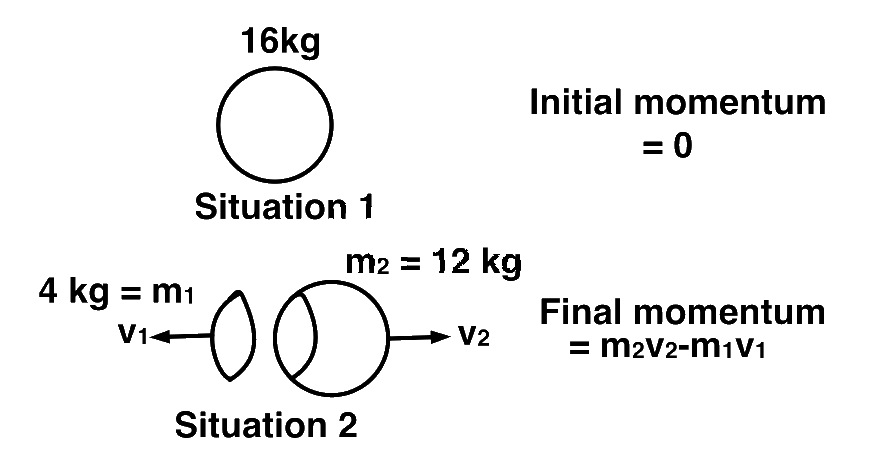
Applying conservation of linear momentum
$$0 = {m_2}{v_2} - {m_1}{v_1}$$
$$\Rightarrow {v_1} = {{12 \times 14} \over 4} = 12\,m{s^{ - 1}}$$
$$\therefore$$ $$K.E{_1} = {1 \over 2}{m_1}v_1^2 = {1 \over 2} \times 4 \times 144 = 288\,J$$
Let the velocity and mass of $$4$$ $$kg$$ piece be $${v_1}$$ and $${m_1}$$ and that of $$12$$ $$kg$$ piece be $${v_2}$$ and $${m_2}$$.

Applying conservation of linear momentum
$$0 = {m_2}{v_2} - {m_1}{v_1}$$
$$\Rightarrow {v_1} = {{12 \times 14} \over 4} = 12\,m{s^{ - 1}}$$
$$\therefore$$ $$K.E{_1} = {1 \over 2}{m_1}v_1^2 = {1 \over 2} \times 4 \times 144 = 288\,J$$
Comments (0)


