JEE MAIN - Physics (2006 - No. 43)
A coin is placed on a horizontal platform which undergoes vertical simple harmonic motoin of angular frequency $$\omega .$$ The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
at the mean position of the platform
for an amplitude of $${g \over {{\omega ^2}}}$$
For an amplitude of $${{{g^2}} \over {{\omega ^2}}}$$
at the height position of the platform
Explanation
Coin $$A$$ is moving in simple harmonic motion in vertical direction. Now we are assuming coin will leave contact with the platform when platform is at a distance of $$x$$ from the mean position which is also called amplitude.
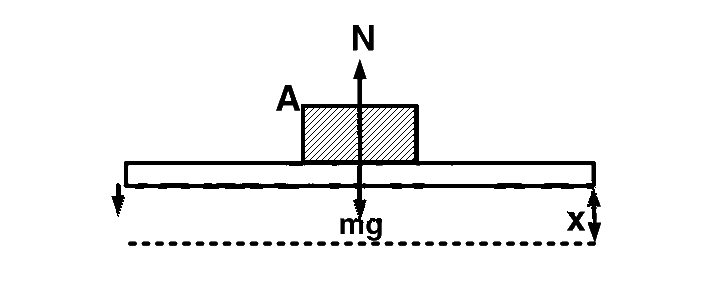
At distance $$x$$ the force acting on the coin is
$$mg - N = m{\omega ^2}x$$
For coin to leave contact $$N=0$$
$$ \Rightarrow mg = m{\omega ^2}x \Rightarrow x = {g \over {{\omega ^2}}}$$
$$\therefore$$ Option (B) is correct.

At distance $$x$$ the force acting on the coin is
$$mg - N = m{\omega ^2}x$$
For coin to leave contact $$N=0$$
$$ \Rightarrow mg = m{\omega ^2}x \Rightarrow x = {g \over {{\omega ^2}}}$$
$$\therefore$$ Option (B) is correct.
Comments (0)


