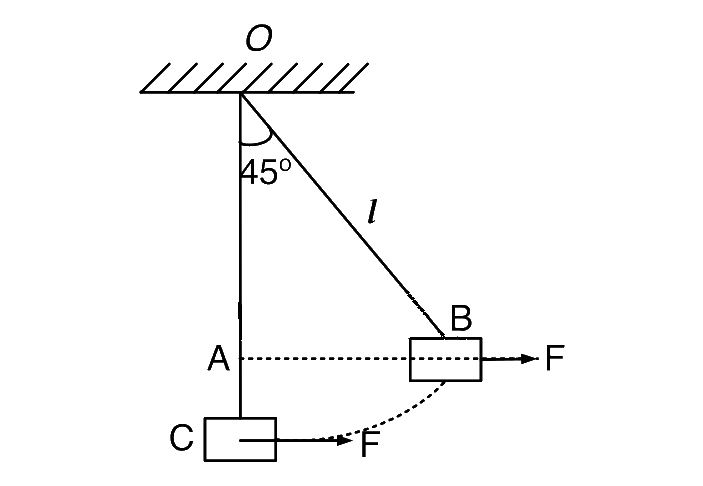From work energy theorem we can say,

Work done by tension $$+$$ work done by force (applied) $$+$$ Work done by gravitational force $$=$$ change in kinetic energy

Here Work done by tension is zero

$$ \Rightarrow 0 + F \times AB - Mg \times AC = 0$$
$$ \Rightarrow F = Mg\left( {{{AC} \over {AB}}} \right) = Mg\left[ {{{1 - {1 \over {\sqrt 2 }}} \over {{1 \over 2}}}} \right]$$
[ as $$AB = \ell \sin {45^ \circ } = {\ell \over {\sqrt 2 }}$$
and $$AC = OC - OA = \ell - \ell \,\cos \,{45^ \circ } = \ell \left( {1 - {1 \over {\sqrt 2 }}} \right)$$
where $$\ell = $$ length of the string. ]
$$ \Rightarrow F = Mg\left( {\sqrt 2 - 1} \right)$$