JEE MAIN - Physics (2005 - No. 58)
A smooth block is released at rest on a $${45^ \circ }$$ incline and then slides a distance $$'d'$$. The time taken to slide is $$'n'$$ times as much to slide on rough incline than on a smooth incline. The coefficient of friction is
$${\mu _k} = \sqrt {1 - {1 \over {{n^2}}}} $$
$${\mu _k} = 1 - {1 \over {{n^2}}}$$
$${\mu _k} = \sqrt {1 - {1 \over {{n^2}}}} $$
$${\mu _s} = 1 - {1 \over {{n^2}}}$$
Explanation
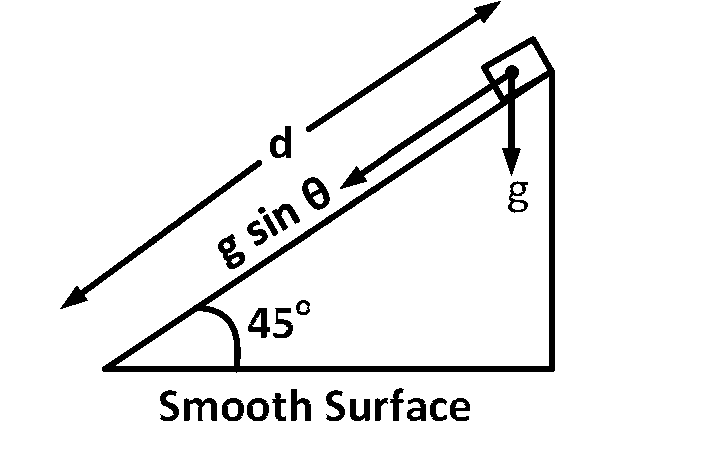
For smooth surface,
$$d = {1 \over 2}\left( {g\,\sin \,\theta } \right)t_1^2,$$
$${t_1} = \sqrt {{{2d} \over {g\,\sin \,\theta }}} ,$$
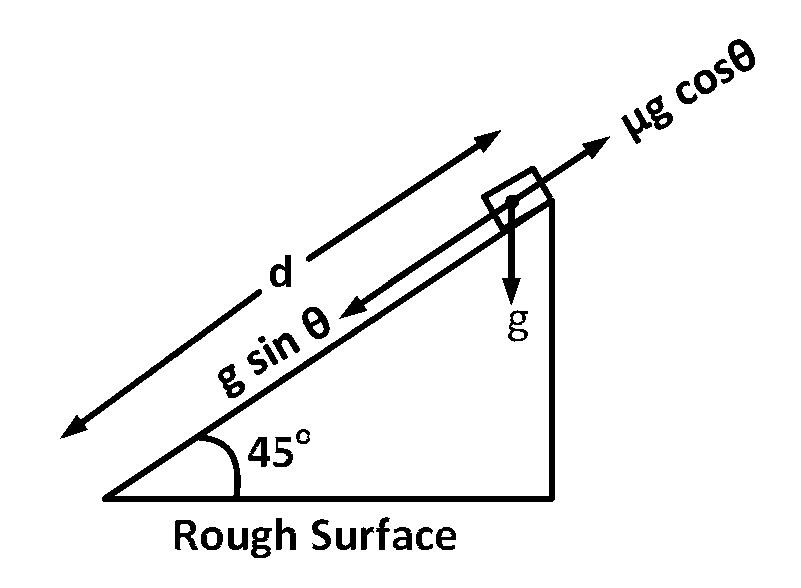
When surface is rough
$$d = {1 \over 2}\left( {g\,\sin \,\theta - \mu g\,\cos \theta } \right)t_2^2$$
$${t_2} = \sqrt {{{2d} \over {g\,\sin \,\theta - \mu g\,\cos \theta }}} $$
According to question, $${t_2} = n{t_1}$$
$$n\sqrt {{{2d} \over {g\,\sin \,\theta }}} = \sqrt {{{2d} \over {g\,\sin \,\theta - \mu g\,\cos \theta }}} $$
$$n = {1 \over {\sqrt {1 - {\mu _k}} }}$$ ( as $$\cos \,{45^ \circ } = \sin \,{45^ \circ } = {1 \over {\sqrt 2 }}$$ )
$${n^2} = {1 \over {1 - {\mu _k}}}$$
or $$1 - {\mu _k} = {1 \over {{n^2}}}$$
or $${\mu _k} = 1 - {1 \over {{n^2}}}$$
Comments (0)


