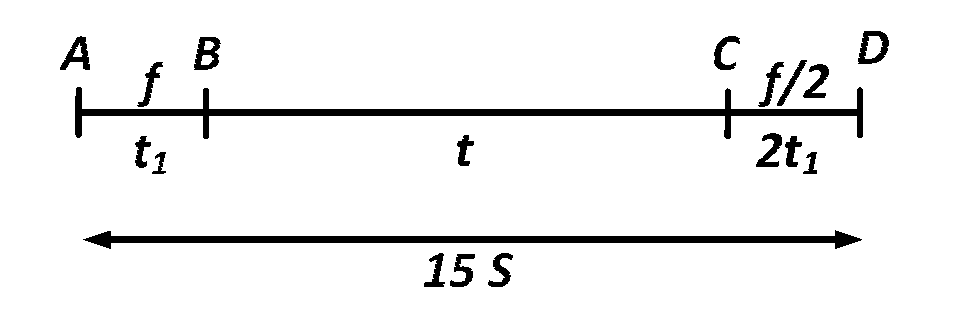Initially car starts from rest so u = 0.

Now distance from $$A$$ to $$B$$,

$$\,\,\,\,\,\,\,\,\,\,$$ $$ S = {1 \over 2}ft_1^2 $$

$$\Rightarrow ft_1^2 = 2S$$

Distance from $$B$$ to $$C$$ $$ = \left( {f{t_1}} \right)t$$

In B to C velocity is constant and v = $${f{t_1}}$$

Distance from $$C$$ to $$D$$
$$\,\,\,\,\,\,\,\,\,\,$$ $$ = {{{u^2}} \over {2a}} = {{{{\left( {f{t_1}} \right)}^2}} \over {2\left( {f/2} \right)}} = ft_1^2 = 2S$$

$$ \Rightarrow S + f\,{t_1}t + 2S = 15S $$

$$\Rightarrow f\,{t_1}t = 12S$$ ........(1)

But$$\,\,\,\,\,\,\,\,\,$$ $${1 \over 2}f\,t_1^2 = S$$ .........(2)

On dividing the above two equations, we get $${t_1} = {t \over 6}$$

$$ \Rightarrow S = {1 \over 2}f{\left( {{t \over 6}} \right)^2} = {{f\,{t^2}} \over {72}}$$