JEE MAIN - Physics (2005 - No. 47)
Two thin wire rings each having a radius $$R$$ are placed at a distance $$d$$ apart with their axes coinciding. The charges on the two rings are $$+q$$ and $$-q.$$ The potential difference between the centres of the two rings is
$${q \over {2\pi \,{ \in _0}}}\left[ {{1 \over R} - {1 \over {\sqrt {{R^2} + {d^2}} }}} \right]$$
$${{qR} \over {4\pi \,{ \in _0}\,{d^2}}}$$
$${q \over {4\pi \,{ \in _0}}}\left[ {{1 \over R} - {1 \over {\sqrt {{R^2} + {d^2}} }}} \right]$$
zero
Explanation
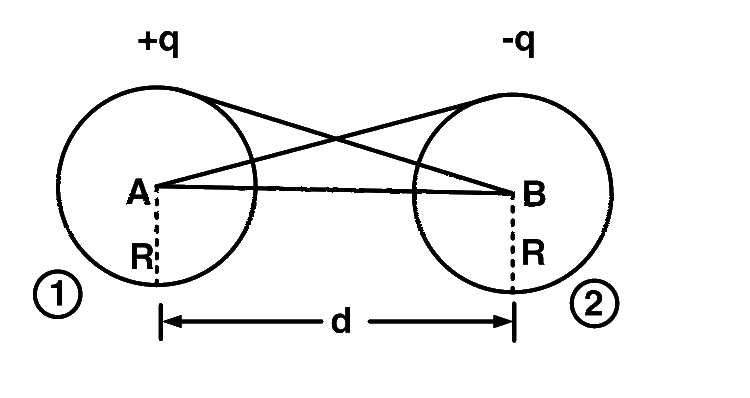
$${V_A} = {V_{self}} + {V_{due}}$$ to $$(2)$$
$$ \Rightarrow {V_A} = {1 \over {4\pi {\varepsilon _0}}}\left[ {{q \over R} - {q \over {\sqrt {{R^2} + {d^2}} }}} \right]$$
$${V_B} = {V_{self}} + {V_{due}}$$ to $$(1)$$
$$ \Rightarrow {V_B} = {1 \over {4\pi {\varepsilon _0}}}\left[ {{{ - q} \over R} + {q \over {\sqrt {{R^2} + {d^2}} }}} \right]$$
$$\Delta V = {V_A} - {V_B}$$
$$ = {1 \over {4\pi {\varepsilon _0}}}\left[ {{q \over R} + {q \over R} - {q \over {\sqrt {{R^2} + {d^2}} }} - {q \over {\sqrt {{R^2} + {d^2}} }}} \right]$$
$$ = {1 \over {2\pi {\varepsilon _0}}}\left[ {{q \over R} - {q \over {\sqrt {{R^2} + {d^2}} }}} \right]$$
Comments (0)


