JEE MAIN - Physics (2005 - No. 38)
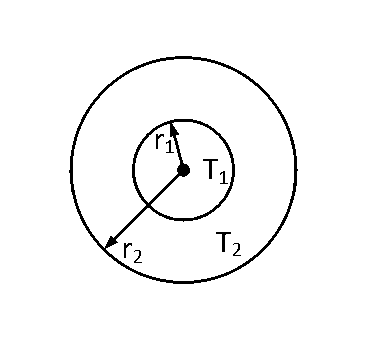
The figure shows a system of two concentric spheres of radii $${r_1}$$ and $${r_2}$$ are kept at temperatures $${T_1}$$ and $${T_2}$$, respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to

$$In\left( {{{{r_2}} \over {{r_1}}}} \right)$$
$${{\left( {{r_2} - {r_1}} \right)} \over {\left( {{r_1}{r_2}} \right)}}$$
$${\left( {{r_2} - {r_1}} \right)}$$
$${{{r_1}{r_2}} \over {\left( {{r_2} - {r_1}} \right)}}$$
Explanation
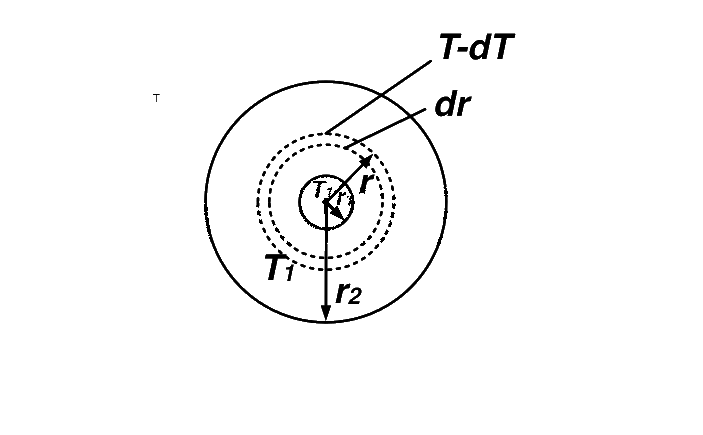
Consider a shell of thickness $$(dr)$$ and of radius $$(r)$$ and the temperature of inner and outer surfaces of this shell be $$T,(T-dT)$$
$$H = {{KA\left[ {\left( {T - dT} \right) - T} \right]} \over {dr}} = {{ - KAdT} \over {dr}}$$
$$H = - 4\pi K{r^2}{{dT} \over {dr}}$$ ( as $$A = 4\pi {r^2}$$ )
Then, $$\left( H \right)\int\limits_{{r_1}}^{{r^2}} {{1 \over {{r^2}}}} dr = - 4\pi K\int\limits_{{T_1}}^{{T_2}} {dT} $$
$$H\left[ {{1 \over {{r_1}}} - {1 \over {{r_2}}}} \right] = - 4\pi K\left[ {{T_2} - {T_1}} \right]$$
or $$H = {{ - 4\pi K{r_1}{r_2}\left( {{T_2} - {T_1}} \right)} \over {\left( {{r_2} - {r_1}} \right)}}$$
Comments (0)


