JEE MAIN - Physics (2005 - No. 33)
A mass $$'m'$$ moves with a velocity $$'v'$$ and collides inelastically with another identical mass. After collision the $${1^{st}}$$ mass moves with velocity $${v \over {\sqrt 3 }}$$ in a direction perpendicular to the initial direction of motion. Find the speed of the $${2^{nd}}$$ mass after collision.

$${\sqrt 3 v}$$
$$v$$
$${v \over {\sqrt 3 }}$$
$${2 \over {\sqrt 3 }}v$$
Explanation
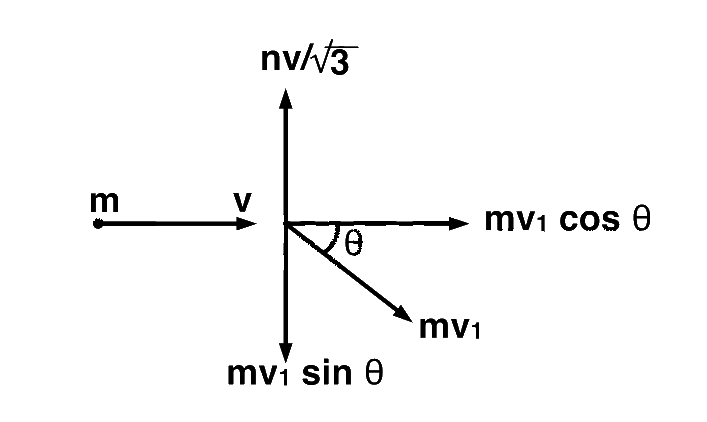
Assume speed of second mass = $${v_1}$$
As momentum is conserved,
In $$x$$-direction, $$mv = m{v_1}\cos \theta \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,....(1)$$
As momentum is conserved,
In $$x$$-direction, $$mv = m{v_1}\cos \theta \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,....(1)$$
In $$y$$-direction, $${{mv} \over {\sqrt 3 }} = m{v_1}\,\sin \theta \,\,\,\,\,\,\,\,\,\,...(2)$$
Squaring and adding eqns.$$(1)$$ and $$(2)$$
$${\left( {m{v_1}\cos \theta } \right)^2} + {\left( {m{v_1}\sin \theta } \right)^2}$$$$ = {\left( {mv} \right)^2} + {\left( {{{mv} \over {\sqrt 3 }}} \right)^2}$$
$$ \Rightarrow $$ $$v_1^2 = {v^2} + {{{v^2}} \over {\sqrt 3 }} $$
$$\Rightarrow {v_1} = {2 \over {\sqrt 3 }}v$$
Comments (0)


